Inhaltsübersicht
Kategorien durchsuchen
Autoren durchsuchen
 AB
ABAlberto Boffi
 AL
ALAlessia Longo
 AH
AHAl Hoge
 AB
ABAljaž Blažun
 BJ
BJBernard Jerman
 BČ
BČBojan Čontala
 CF
CFCarsten Frederiksen
 CS
CSCarsten Stjernfelt
 DC
DCDaniel Colmenares
 DF
DFDino Florjančič
 EB
EBEmanuele Burgognoni
 EK
EKEva Kalšek
 FB
FBFranck Beranger
 GR
GRGabriele Ribichini
Glacier Chen
 GS
GSGrant Maloy Smith
 HB
HBHelmut Behmüller
 IB
IBIza Burnik
 JO
JOJaka Ogorevc
 JR
JRJake Rosenthal
 JS
JSJernej Sirk
 JM
JMJohn Miller
 KM
KMKarla Yera Morales
 KD
KDKayla Day
 KS
KSKonrad Schweiger
Leslie Wang
 LS
LSLoïc Siret
 LJ
LJLuka Jerman
 MB
MBMarco Behmer
 MR
MRMarco Ribichini
 ML
MLMatic Lebar
 MS
MSMatjaž Strniša
 ME
MEMatthew Engquist
 ME
MEMichael Elmerick
 NP
NPNicolas Phan
 OM
OMOwen Maginity
 PF
PFPatrick Fu
 PR
PRPrimož Rome
 RM
RMRok Mesar
 RS
RSRupert Schwarz
 SA
SASamuele Ardizio
 SK
SKSimon Kodrič
 SG
SGSøren Linnet Gjelstrup
 TH
THThorsten Hartleb
 TV
TVTirin Varghese
 UK
UKUrban Kuhar
Valentino Pagliara
 VS
VSVid Selič
 WK
WKWill Kooiker
Modalanalyse: Der ultimative Ratgeber

September 26, 2025
In diesem Artikel befassen wir uns mit Strukturdynamik, Modaltests und Modalanalyse, und zwar so detailliert, dass Sie:
Verstehen, was eine Modalanalyse ist und wozu sie dient;
Lernen, wie eine Modalanalyse durchgeführt wird;
Erkennen, wie eine Modalanalyse funktioniert.
Die nachstehende Inhaltsangabe gibt einen Überblick über diesen Artikel mit den behandelten Themen in der gleichen Reihenfolge, in der eine normale Modalanalyse durchgeführt werden würde.
Einführung in die Welt der Modal Analyse
Was ist eine Modalanalyse?
Die Modalanalyse ist ein unverzichtbares Werkzeug für das Verständnis der Strukturdynamik von Objekten – wie Strukturen und Objekte schwingen und wie widerstandsfähig sie gegen einwirkende Kräfte sind. Sie dient zum Testen, Optimieren und Validieren von Konstruktionen.
Die Modalanalyse hat sich in zahlreichen Anwendungen in der Automobilindustrie, im Bauwesen, in der Luft- und Raumfahrt, in der Energieerzeugung, in der Musikinstrumentenindustrie und in anderen Bereichen bewährt.
Es können Eigenresonanzfrequenzen der Objekte und Dämpfungsparameter berechnet und Eigenformen auf einem animierten geometrischen Modell der Messobjekte visualisiert werden.
Gesammelt werden die Modalparameter (Eigenfrequenz, Dämpfung und Eigenform) als Modalmodell bezeichnet.
Zur Ermittlung korrekter Modalmodelle müssen sorgfältige Modalanalysen auf der Grundlage genauer Modaltestmessungen durchgeführt werden.
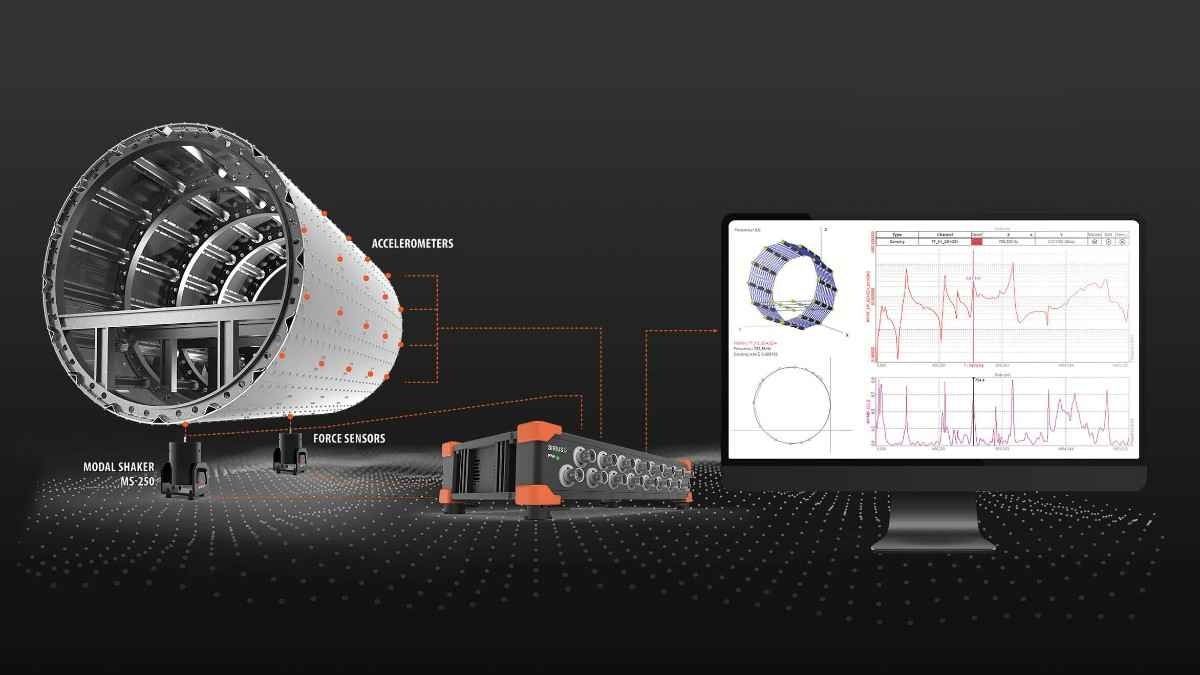
Bei Modaltests und -analysen kommen üblicherweise zum Einsatz:
ein oder mehrere Schwingungsanreger, wie Modalshaker oder Impulshammer
Kraftsensoren zur Erfassung der Anregungssignale
Beschleunigungssensoren zur Erfassung der Antwortsignale
ein Datenerfassungsgerät
ein Computer mit einer Softwareanwendung für Modaltest und -analyse
Erfahren Sie mehr:

Wozu dient eine Modalanalyse?
Die Modalanalyse wird in den verschiedensten Branchen häufig eingesetzt, etwa zur Analyse und Validierung von Flugzeugrahmenteilen, Wind- oder Gasturbinenschaufeln, Fahrgestellen oder jeder Art von anderen Konstruktionen, die Kräften ausgesetzt sind und Resonanzfrequenzen mit kritisch niedriger Dämpfung aufweisen können.
Bei Resonanzfrequenzen mit kritisch niedriger Dämpfung reagiert und schwingt ein Objekt stark schon bei geringer Kraft- und Energiezufuhr.
Die Modalanalyse kann dem Anwender einen Überblick über die Eigenfrequenzen, Dämpfungsparameter und strukturellen Schwingungsformen des Objekts geben. Mit seiner Hilfe kann der Anwender das Objekt so modifizieren, dass es weniger empfindlich auf einwirkende Kräfte reagiert, und das Objektdesign, z. B. hinsichtlich der Form und Masse, optimieren.
Die Modalanalyse wird auch verwendet, um analytische Finite-Elemente-Modelle mittels der durch Modaltests ermittelten Dämpfungseigenschaften mit realen Prototypen zu korrelieren.
Die Designoptimierung steht oft im Fokus, wenn es um die Erfüllung neuer Anforderungen, etwa bei der Kraftstoffeinsparung und für leichtgewichtigere Strukturen, geht. Eine strukturdynamische Analyse ist bei solchen Prozessen meist zwingend erforderlich, um in Erfahrung zu bringen, wie die Struktur auf eine bestimmte Optimierung reagiert.
Wie wird eine Modalanalyse durchgeführt?
Für den Erhalt qualitativ hochwertiger Modaldaten und damit eine Modalanalyse ihren Zweck erfüllen kann, sind zahlreiche Testaspekte zu berücksichtigen.
In der Regel handelt es sich dabei um die folgenden Aspekte, die in diesem Artikel näher beschrieben werden:
Modaltest
Vorbereitung
Ausrüstung
Vorversuche
Geometrie
Freiheitsgrade (DOF)
Anregungstechnik
Konfiguration
Messungen
Frequenzgangfunktion (FRF)
Betriebsschwingformanalyse (ODS)
Validierung
Kohärenz
Modalanalyse
Parameteridentifikation
Eigenfrequenz-Indikator-Funktionen (MIF)
Kurvenanpassung
Modenauswahl
Stabilitätsdiagramm
Eigenfrequenzen
Dämpfung
Eigenformen
Modellvalidierung
AutoMAC und CrossMAC
Skalierung der Eigenformen
Synthese
Die Modalanalyse kann auf Testmessungen an der Struktur oder simulierten Finite-Elemente-Modellen (FEM) basieren. Dieser Artikel konzentriert sich im Wesentlichen auf die Modalanalyse auf Grundlage realer Modaltest-Ergebnisse. Die Analyse der Korrelation zwischen simulierten Finite-Elemente-Modellen und Testergebnissen ist eine Erweiterung der Modalanalyse, die wir in einem anderen Artikel behandeln werden.
Was sind Modaltests?
Modaltests und die erfassten Testdaten bilden die Grundlage für die Durchführung von Modalanalysen und das Ziehen von Rückschlüssen auf die Strukturdynamik von Testobjekten.
Dieser Abschnitt enthält ausreichende Informationen für ein grundlegendes Verständnis von Modaltests und der Erfassung von Daten für eine anschließende Modalanalyse.
Weitere Informationen zu Modaltests finden Sie in Quelle 1.1.
Modaltests können entweder mit künstlichen Anregungsquellen durchgeführt werden, die das Testobjekt in Schwingung versetzen, oder indem man den Prüfling unter operationellen Bedingungen testet (Vor-Ort-Test), bei denen die üblichen Schwingungen auftreten.
Weitere Infos:

Experimentelle Modalanalyse (EMA)
Die experimentelle Modalanalyse (EMA) kann sowohl vor Ort als auch in einer kontrollierten Laborumgebung durchgeführt werden, wobei ein Labor den Vorteil eines besseren Signal-Rausch-Verhältnisses (SNR) sowie der Möglichkeit zur einfachen Änderung der Testanordnung bietet.
Bei der EMA werden Objekte durch künstliche Kräfte angeregt und dann sowohl die Eingangssignale (Anregungen) als auch die Ausgangssignale (Antworten) gemessen und zum Aufbau der Modalmodelle verwendet.
Betriebsschwingformanalyse (ODS)
Die Betriebsschwingformanalyse (Operating Deflection Shape, ODS) ist eine einfache Möglichkeit zur Durchfûhrung dynamischer Analysen, um zu sehen, wie sich eine Maschine oder eine Struktur unter operationellen Bedingungen bewegt. Beim ODS-Test kommen keine künstlichen Kräfte zur Anwendung, und es werden nur die Antwortschwingungssignale gemessen.
ODS-Messungen reichen zum Aufbau eines Modalmodells nicht aus, liefern jedoch strukturelle Schwingformen, die die Strukturanalyse von Prüflingen (auch Device Under Test, DUT) unter operationellen Bedingungen erleichtern.
Die ODS wird erfolgreich zur Überwachung von Maschinenzuständen und im Bauwesen eingesetzt, z. B. an Brücken, Gebäuden und anderen Strukturen, bei denen eine Anregung durch künstliche Kräfte nur schwer zu bewerkstelligen ist.
Betriebsmodalanalyse (OMA)
Messtechnisch ähnelt das Verfahren für die Betriebsmodalanalyse (OMA) dem für die ODS, wobei der Analyseteil jedoch abweicht. Wie sich die ODS und die OMA unterscheiden, wird im Abschnitt „Modalanalyse“ dieses Artikels beschrieben.
Testvorbereitung
Vor Beginn eines Modaltests sind gewisse Vorbereitungen erforderlich. Dazu zählen:
Mounting of the Test Structure
Type of excitation force(s)
Location(s) of excitation (driving points)
Hardware and sensors to measure the force(s) and responses
Geometry Model
Auswahl des Auflagers der Struktur
Bei der Durchführung von Modaltests muss der Prüfling (DUT - Device Under Test) frei schwingen können, damit alle Eigenfrequenzen und Modenformen der Struktur sichtbar werden.
Gerade im reellen Umfeld werden häufig Materialien wie Gummibänder, elastische Aufhängungen, Schaumstoffpolster und andere Materialien verwendet um eine entkoppelte Montage zu ermöglichen.
Ohne diese Entkoppelung verschieben sich die gemessenen Frequenzen nach oben und manche Modenformen würden gar nicht erkannt werden.
Starre Körperbewegung
Starre Bewegungen oder Starrkörpermodi sind Schwingungen des gesamten Prüflings als gesamtes/starres Objekt und liefern keine Informationen über die strukturdynamischen Eigenschaften des Prüflings (also über die flexiblen Modi). Solche Starrkörpermodi hängen mit der ausgewählten Aufhängung des Prüflings zusammen.
Abhängig davon, wie dieser montiert ist, können die Starrkörpermodi die flexiblen Modi der Struktur zu stark beeinflussen. Der Einfluss der starren Moden auf die flexiblen Moden hängt davon ab, wie nahe diese an den flexiblen Moden liegen und was als akzeptable Genauigkeit der Messungen bestimmt wird.
Als Faustregel für akzeptable Modaldaten gilt es, wenn die FRFs ein Frequenzverhältnis von mehr als 10:1 zwischen den Starrkörpermoden und den flexiblen Moden aufweisen, z.B. letzter starrer Modus bei 1 Hz und erster flexibler Modus bei 10 Hz. Dies ist aber von der gewünschten Genauigkeit abhängig. Oft wird die Aufhängung zwischen den Messvorgängen verändert um deren Beeinflussung besser beurteilen zu können.
Art der Anregungskraft (oder -kräfte)
Für EMA-Tests können verschiedene Anregungsarten gewählt werden. Die beste Wahl hängt vom jeweiligen Anwendungsszenario ab. Zum Beispiel:
Die Impulshammer-Methode ist oft die beste Lösung für kleinere, homogene Strukturen und für Vor-Ort-Messungen, da sie schnell und mobil ist und keine Einspannung des Testobjekts erfordert.
Sinus-Sweeps, Zufallsrauschen und andere Arten der Anregung mittels eines Modalshakers sind oft die beste Lösung für größere, komplexe Strukturen, die eine tiefergehende Analyse (z. B. mit Nichtlinearitätsstudien, einem niedrigen Scheitelfaktor oder einem hohen Signal-Rausch-Verhältnis) erfordern. Durch gezielte langsame Sweeps in einem eingeschränkten Frequenzbereich bekommt man außerdem mehr Energie in die einzelnen Frequenzpunkte.
Für komplexe Strukturen können mehrere Shaker erforderlich sein, wenn keine Anregungsstellen (Referenz-DOF) gefunden werden können, an denen alle Moden eine für den Aufbau eines korrekten Modalmodells ausreichend hohe Beteiligung haben. Darüber hinaus lässt sich mit Modalshakern der Kraftpegel präzise kontrollieren.
In einigen anderen Szenarien sollten nicht standardisierte Schwingungsquellen, wie z. B. elektrohydraulische Shaker oder Fallhämmer, zusammen mit anderen Anregungsmethoden verwendet werden, die für bestimmte Zwecke besser geeignete Anregungssignale liefern.
Anregungsstellen (Referenzpunkte)
Bei EMA-Tests ist es wichtig, das Objekt an einer oder mehreren Stellen anzuregen, die sich so auf das Objekt auswirken, dass sich die meisten Schwingungseigenschaften offenbaren. Versucht man zum Beispiel, ein Objekt an einer Stelle anzuregen, an der einige Schwingungsmodenmuster immer eine minimale Schwingungsamplitude aufweisen, dann nehmen diese Moden keine Energie auf und werden nicht angeregt.
Um geeignete Anregungsstellen zu identifizieren, sind oft Vorversuche erforderlich, bei denen verschiedene Referenzpunkte (Driving Points) verglichen werden. Wenn ein Finite-Elemente-Modell (FEM) zur Verfügung steht, kann auch dieses zur Bestimmung geeigneter Anregungsstellen verwendet werden.
Für ODS- und OMA-Tests, bei denen keine Krafteingangssignale verwendet werden, ist es ebenso wichtig, die Antwortsensoren so zu positionieren, dass sie nicht in den Knotenpunkten einer Schwingmode liegen, und somit bei Anregung eine ausreichende Amplitude herrscht.
Hardware und Sensoren für die Impuls- und Impulsantwortmessung
Bei EMA-Tests werden die Anregungssignale üblicherweise mit Kraftaufnehmern oder Impedanzköpfen an den Referenzpunkten gemessen. Ein Impedanzkopf enthält sowohl einen Kraft- als auch einen Beschleunigungssensor und wird oft zur Referenzpunktmessung verwendet.
Als Alternative zu Impedanzköpfen kann ein Beschleunigungssensor in der Nähe des Kraftsensors an den Anregungspunkten platziert werden. Antwortsignale werden sehr häufig mit Beschleunigungssensoren gemessen, es können aber auch andere Sonden verwendet werden.
Oft werden mehrere Beschleunigungssensoren eingesetzt, um die Datenkonsistenz zu optimieren und die Messzeit zu verkürzen, und bei größeren komplexen Strukturen kann die Anzahl dieser Sensoren schnell ziemlich groß werden.
Ist die Anzahl der Antwortsensoren begrenzt, dann kann eine „wandernde Messung“ (roving measurement) verwendet werden. Bei Roving-Accelerometer-Messungen wird eine Gruppe von Antwortsensoren zur Durchführung von Teilmessungen mehrfach umpositioniert, bis alle DOF-Positionen vollständig gemessen sind.
In den Fällen, in denen verschiedene Moden Auslenkungen in verschiedene orthogonale Richtungen aufweisen, kann es von Vorteil sein, dreiachsige Beschleunigungssensoren für die Modaltests zu verwenden.
Diese Sensoren haben unterschiedliche Empfindlichkeiten und decken unterschiedliche Frequenzbereiche ab. Sie sollten so gewählt werden, dass sie alle den im Modaltest verwendeten Frequenz- und Amplitudenbereich unterstützen. Diese Dynamikbereiche müssen auch von der gewählten Datenerfassungshardware nterstützt werden.
Bei leichten Strukturen ist außerdem auch das Gewicht der Sensoren zu berücksichtigen, damit sich die Schwingformen nicht durch die Massenbelastung der Sensoren verändern. Als Faustregel gilt, dass die Masse des Sensoren weniger als 1/10 der Masse des Testobjekts betragen sollte.
Hier finden Sie das passende Dewesoft Messsystem für Datenerfassung in höchster Qualität
Mehr erfahren:
Geometrisches Modell
In den meisten Fällen sollte vor Beginn eines Modaltests ein geometrisches Modell erstellt werden.
Die Geometrie wird durch Punkte, Verbindungslinien und Flächen erzeugt, wobei einige Punkte den zu messenden Stellen entsprechen, die auch als DOF (Degrees Of Freedom oder Freiheitsgrade) bezeichnet werden. DOF definieren die Knotenpunktpositionen und die zu messenden Richtungen, z. B. '0012, Z+'.
Geometrische Modelle werden z. B. verwendet, um bei der Auswahl des besten DOF-Satzes für die Messung zu helfen, um einen Überblick über den Messprozess zu geben und ihn zu steuern und um die ermittelten Schwingungsmuster des Testobjekts zu visualisieren.
Wie wird ein Modaltest durchgeführt?
Nach Abschluss der Testvorbereitungen kann der Modaltest beginnen. Für EMA-Tests ist es je nach Prüfsituation möglich, einen oder mehrere Modalanreger und einen oder mehrere Antwortsensoren zu verwenden. Diese unterschiedlichen Testkonfigurationen werden in den Abschnitten „Einzel-Referenz-Modaltests“ und „Multi-Referenz-Modaltests“ beschrieben. Ein anschließender Abschnitt befasst sich mit ODS-Tests.
Einzel-Referenz-Modaltests
In einigen Testfällen reichen die Messdaten von einem einzigen Referenz-DOF zum Aufbau des Modalmodells aus.
Dabei wird davon ausgegangen, dass der ausgewählte Referenz-DOF Informationen über alle Moden enthält. Dies ist möglich, wenn die Position des Referenz-DOF so gewählt werden kann, dass sie für keine Mode auf einem Knotenpunkt liegt. In der Praxis bedeutet dies, dass alle Moden in den Messdaten im ausreichenden Umfang „präsent“ sein sollten.
Impulshammer-Methode, Einzel-Referenz
Für einen Roving-Hammer-Test bedeutet dies, dass nur ein Antwort-DOF, also nur eine Beschleunigungssensorposition, erforderlich ist. Dabei wird der Beschleunigungssensor-Antwort-DOF als Referenz-DOF verwendet, während der Hammer zwischen den DOF „hin- und herwandert“. Dies ist ein Beispiel für eine sogenannte SISO-Testkonfiguration (Single Input, Single Output).
Wandernder-Beschleunigungssensor-Test, Einzel-Referenz
Es kann auch eine andere Roving-Testart gewählt werden, bei dem der Schwingungsanreger (z. B. Hammer oder Shaker) als Referenz-DOF verwendet wird, während ein oder mehrere Beschleunigungssensoren so lange umpositioniert werden, bis alle DOF angeregt und gemessen sind. Dies wird auch als „Roving Response Test“ bezeichnet.
Bei Verwendung mehrerer Beschleunigungssensoren spricht man von einer SIMO-Testkonfiguration (Single Input, Multiple Output).
Der Nachteil dieser Konfiguration ist, dass bei leichten Strukturen die Masse des Beschleunigungssensors an jedem Punkt anders auf die Struktur einwirkt und somit die Messung beeinflusst (Mass-Loading-Effekt).
Außerdem muss der Sensor zwischen den einzelnen Messungen bewegt und erneut montiert werden, wodurch sich der zeitliche Aufwand im Vergleich zum Roving-Hammer-Test erhöht.
Shaker-Test, Einzel-Referenz
Für einen Einzel-Referenz-Modaltest (bei dem ein einziger Referenz-DOF für den Aufbau des Modalmodells ausreicht) kann auch ein Modalshaker verwendet werden.
Ein Modalshaker wird häufig für Modaltests gewählt, die eine genauere Bestimmung des Modalmodells erfordern.
Bei der Verwendung eines Modalshakers wird die Referenz-DOF meist als Anregungsstelle für den Shaker gewählt, z. B. da es in der Regel zeitaufwändiger ist, den Shaker umzupositionieren als eine Gruppe von Beschleunigungssensoren.
Multi-Referenz-Modaltests
Einige Testfälle erfordern Messungen mit mehr als einem Referenz-DOF. Dies ist der Fall, wenn kein geeigneter Referenz-DOF gefunden werden kann, bei dem alle Moden im ausreichenden Umfang in den Messdaten „präsent“ sind.
Die Struktur könnte z. B. an verschiedenen Teilen unterschiedliche Moden mit verschiedenen vorherrschenden modalen Auslenkungen aufweisen. Solche Moden werden auch als „lokale Moden“ bezeichnet.
Ein Beispiel hierfür sind komplexe Strukturen, die aus mehreren verschiedenen Teilen mit unterschiedlichen strukturellen Eigenschaften bestehen.
Ein Multi-Referenz-Test ist auch erforderlich, wenn das Testobjekt mehrere Moden mit übereinstimmender Resonanzfrequenz aufweist. In diesen Fällen spricht man von „Repeated Roots“ oder „eng benachbarten Moden“.
Ein Beispiel für Repeated Roots ist das Vorhandensein bestimmter symmetrischer Strukturen. Dabei können z. B. zwei senkrecht zueinander ausgerichtete Biegemoden hinsichtlich ihrer Resonanzfrequenz eng benachbart sein.
Die Anzahl der gemessenen Referenz-DOF muss (mindestens) der Anzahl der Moden bei gleicher Frequenz entsprechen.
Wandernder-Hammer-Test, Multi-Referenz
Bei Hammertests kann die Einbeziehung mehrerer Referenz-DOF in einen Modaltest durch die Verwendung mehrerer Antwortsensoren als Referenz-DOF bewerkstelligt werden.
Multi-Referenz-Shaker-Test
Tests mit mehreren Shakern werden in der Regel auch mit mehreren Beschleunigungssensoren durchgeführt – also mit einer MIMO-Konfiguration (Multiple Input, Multiple Output).
Der Hauptvorteil der Verwendung mehrerer Shaker besteht in der Verteilung der Energie der einwirkenden Kraft auf zusätzliche Stellen an der Struktur. Dies führt insbesondere bei großen und komplexen Strukturen und bei Strukturen mit starker Dämpfung zu einer gleichmäßigeren Schwingungsantwort über die Struktur.
In der Absicht, bei solchen Strukturen eine ausreichende Schwingungsenergie zu erzeugen, wird der die Amplitude der Anregung bei Verwendung eines einzigen Shakers oft zu hoch gewählt. Dies kann zu nicht-linearen Effekten und einem mangelhaften Aufbau des Modalmodells führen. Die Anregung an mehreren Stellen liefert oft auch eine bessere Darstellung der Anregungskräfte, die im realen Betrieb auf die Struktur einwirken.
Die Verwendung mehrerer Shaker anstelle eines einzigen wandernden Shakers hat zudem den Vorteil konsistenterer Daten und einer kürzeren Messzeit. Bei einer mit den Daten eines Multi-Referenz-Modaltests durchgeführten Modalanalyse ist die Datenkonsistenz von entscheidender Bedeutung.
Bei der Verwendung mehrerer Modalshaker werden die Anregungssensoren als Referenz-DOF verwendet.
Unterscheidbare Moden an den Referenz-DOF
In Multi-Referenz-Konfigurationen müssen die zu extrahierenden Eigenformen an den Referenz-DOF „unterschiedlich aussehen“. Das heißt, die Eigenformen für diese Moden müssen an den Referenz-DOF linear unabhängig sein. Dies wird durch die Auswahl geeigneter Referenz-DOF gewährleistet.
So könnte eine Platte zwei eng benachbarte Moden (mit ungefähr gleicher Resonanzfrequenz) haben, für die die Auslenkung an einigen DOF ähnlich ist. Werden nun zwei solcher DOF mit ähnlichem Schwingungsmuster als Referenz-DOF gewählt, dann enthalten die gemessenen Referenz-DOF-Daten keine Informationen, mit denen diese Moden getrennt werden können.
Multi-Referenz-Anregungsarten
Bei Multi-Referenz-Shaker-Tests werden in der Regel unkorrelierte zufällige Anregungssignalarten verwendet. Diese stochastischen Anregungsarten können verschiedene Verläufe (kontinuierlich, Burst oder periodisch) haben.
Sinusförmige Anregungssignale können auch dazu verwendet werden, Sinustests (z. B. Stufensinus-Tests oder Normalmoden-Abstimmungen) durchzuführen.
Bei Sinustests ist es möglich, den Anregungskraftpegel für eine bestimmte Frequenz an den einzelnen Anregungs-DOF zusammen mit dem Phasenmuster zwischen ihnen zu steuern.
Die Möglichkeit, die Anregungsamplitude und das Phasenmuster an DOF zu steuern, erlaubt es, sich auf eine bestimmte Mode "einzustellen" (Normalmoden-Abstimmung). Dies kann sehr interessant sein, wenn eine detaillierte Untersuchung einzelner Moden gewünscht ist, also z. B. zur Durchfûhrung einer Nichtlinearitätsuntersuchung spezifischer Moden.
Außerdem kann bei Sinustests die gesamte eingesetzte Energie auf die Anregung jeweils nur einer spezifischen Mode konzentriert werden. So lässt sich im Vergleich zu zufälligen Anregungssignalen, bei denen sich die Energie über die gesamte Frequenzspanne verteilt und damit alle Moden gleichzeitig abdeckt, ein erheblicher Teil der eingesetzten Energie einsparen (oder auf eine Frequenz bündeln).
Betriebsschwingformanalyse (ODS)
Die Betriebsschwingformanalyse (Operating Deflection Shape, ODS) ist ein wertvolles Werkzeug für die Analyse vorherrschender Strukturschwingungen unter operationellen Bedingungen an Strukturen, an denen eine normale EMA nur schwer durchführbar ist, und für die Ermittlung geeigneter Veränderungen.
Beispiele für operationelle Testbedingungen können z. B. kontinuierliche Signale von einem laufenden Motor oder transiente Signale von Erdbeben, Explosionen, Falltests oder anderen Ereignissen sein.
Die ODS-Analyse bestimmt die strukturellen Schwingformen eines Prüflings unter operationellen Bedingungen anhand gemessener Amplituden- und Phaseninformationen der DOF.
Für die ODS-Analyse werden keine Anregungs-, sondern ausschließlich Antwortsignale verwendet. Einer oder mehrere Antwort-DOF werden als Referenz-DOF zur Extraktion der Phaseninformation ausgewählt.
Es ist zu beachten, dass die ausgewählte(n) Referenz(en) die Wirkungen aller relevanten Frequenzen/Ordnungen abdecken müssen.
Die Schwingformen können durch Zeitbereichs-ODS, Spektral-ODS oder nicht-stationäre ODS (für Tests mit variabler Geschwindigkeit) bestimmt werden. Die aus den ODS resultierenden Schwingungsmuster werden in allen Fällen in Form animierter geometrischer Modelle und der zugehörigen Amplituden- und Phaseninformationen dargestellt.
Zeitbereichs-ODS
Die Ergebnisse von Zeitbereichs-ODS zeigen sämtliche Schwingungsmuster des in Betrieb befindlichen Prüflings, wobei der Anwender den Zeitbereich definieren kann, über den die Auslenkungen betrachtet werden sollen.
Bei der Zeitbereichs-ODS werden die gemessenen Zeitsignale der DOF verwendet, um die Amplitudenpegel und die Phase bezogen auf die Referenz-DOF zu extrahieren. Dies geschieht für alle Zeitpunkte, und die Auslenkungen können hierbei über eine Zeitachse animiert werden.
Es ist zu beachten, dass die Verwendung der Zeitbereichs-ODS bei der Durchführung von Roving-Accelerometer-Tests problematisch ist, da sie Zeitsignale zur Extraktion der Phaseninformation verwendet. In solchen Fällen sind genaue Triggermechanismen erforderlich, um sicherzustellen, dass alle Roving-Messreihen in Bezug auf die Phaseninformation synchronisiert sind. Normalerweise wird die Zeitbereichs-ODS durchgeführt, wenn genügend Beschleunigungssensoren zur Ausstattung des Prüflings vorhanden sind und kein Roving erforderlich ist.
Spektral-ODS
Die Ergebnisse von Spektral-ODS zeigen die Auslenkungen des Prüflings bei einzelnen, vom Benutzer festgelegten Frequenzen.
Die Spektral-ODS verwendet die verarbeiteten Frequenzdaten der DOF, um die Amplitude und die Phase bezogen auf die Referenz-DOF zu extrahieren. Dies geschieht für alle Frequenzkomponenten in den Spektraldaten, und die Schwingformen können hierbei über eine Frequenzachse animiert werden.
Nicht-stationäre ODS
Die Ergebnisse nicht-stationärer ODS zeigen in der Regel die Auslenkungen des Prüflings bei einzelnen, vom Benutzer festgelegten Drehordnungen.
Bei der nicht-stationären ODS werden üblicherweise dynamische, neu abgetastete (order tracked) Spektraldaten der DOF verwendet, um die Amplitude und die Phase bezogen auf die Referenz-DOF zu extrahieren. Dies geschieht für alle Ordnungskomponenten in den rotationsbezogenen Spektraldaten, und die Auslenkungen können hierbei über eine Ordnungsachse animiert werden.
Mehr erfahren:

Unterschiedliche rotierende Komponenten (wie Zahnräder und Lager) eines Prüflings drehen sich oft in verschiedenen Ordnungen oder Anteilen der gemessenen Drehzahl(en). Sie werden mit unterschiedlichen, drehzahlunabhängigen Ordnungsanteilen angezeigt. Hierbei können die Schwingformen durch Betrachtung der verschiedenen Ordnungen auf verschiedene rotierende Prüflings-Komponenten fokussiert werden.
Wenn sich die Schwingform einer Harmonischen mit der Drehzahl ändert, deutet dies darauf hin, dass Geschwindigkeitsänderungen sich auf die betreffende Komponente auswirken.
Mittelung bei Testmessungen
Bei Durchführung mehrerer Messungen an denselben DOF-Positionen muss ein Mittelwert gebildet werden.
Jede Messung enthält ein gewisses Zufallsrauschen, das die Bestimmung der Resonanzfrequenzen und Eigenformen des Systems beeinflussen kann, diese stochastische Rauschkomponente lässt sich aber durch die Mittelung über mehrere Messungen reduzieren.
Das Zufallsrauschen wird umso stärker reduziert, je mehr Werte gemittelt werden, und es ist Sache des Anwenders, eine geeignete Anzahl von Messblöcken für die Mittelung festzulegen (z. B. um ein ausgewogenes Verhältnis zwischen der Ergebnisqualität und der erforderlichen Testzeit zu gewährleisten).
Als Faustregel gilt, dass bei Shaker-Tests
32–64 Messwerte und bei
Impulshammertests 4–8 Messwerte gemittelt werden sollten.
Normalerweise lässt die Modaltest-Anwendungssoftware den Benutzer die Anzahl der zu mittelnden Werte für jede DOF-Messung festlegen. Für normale Impulshammertests (ein Schlag pro Messblock) bedeutet dies zum Beispiel, dass der Benutzer jede DOF-Position mit einer Schlagzahl anregen sollte, die der angegebenen Anzahl zu mittelnder Werte entspricht.
Die Betrachtung von Kohärenzfunktionen ist ein primäres Validierungswerkzeug bei der Durchführung von Modaltests; lassen Sie sich jedoch nicht von einem Kohärenzwert von 1 nach der ersten Messung in die Irre führen.
Definitionsgemäß basiert die Kohärenzfunktion auf mehreren Messungen und liefert daher erst dann nützliche Daten, wenn eine Mittelung durchgeführt wurde.
Diese Mittelung sollte über die Daten für die einzelnen DOF-Positionen erfolgen und nicht über alle DOF.
Zum Beispiel: Mittelung der Autospektren G_AA (f) und G_BB (f) und der Kreuzspektren G_AB (f) auf Grundlage derselben DOF. Modaldaten wie FRFs und Kohärenzfunktionen werden dann anhand dieser gemittelten Spektren berechnet. Autospektren und Kreuzspektren werden im Anhang näher beschrieben.
Was ist ein Modalhammer?
Ein Modalhammer wird für Impulshammertests (üblicherweise an einfachen Strukturen) oder für schnelle Sondierungen vor der Durchführung eines komplexeren Modalshaker-Test verwendet. Er erfordert relativ wenig Ausrüstung, nämlich einen Sensor, und keine Befestigung eines Shakers an der Struktur. In der Regel ist der zeitliche Aufwand für den Aufbau und die Durchführung eines Modaltests gering, wenn eine geringe Anzahl von Messpunkten ausreicht.
Modalhammertypen
Modalhämmer haben unterschiedliche Größen und Spezifikationen, je nachdem, welche Arten von Strukturen angeregt werden sollen.
Um einen Überblick zu bekommen, welcher Modalhammer für eine bestimmte Aufgabe am besten geeignet ist, kann die folgende Tabelle als Richtschnur dienen.
| Hammer-Größe | Anwendungsbereiche | Bereichsskala | Empfindlichkeit | Gewicht |
|---|---|---|---|---|
| Klein | Kleine Strukturen:Leiterplatten, Prozessoren, Speichermodule und andere empfindliche Objekte | < 100 lbf pk, < 444 N pk | > 50 mV / lbf, >11,2 mV / N | < 0,36 lb, < 0,16 kg |
| Mittel | Mittelgroße Strukturen:Fahrzeugrahmen, Motorblöcke, kleine Elektromotoren und andere mittelschwere Geräte | 100 - 1,00k lbf, pk, 444 - 4,44k N pk | 50 - 5 mV / lbf, 11,2 - 1,10 mV / N | 0,36 - 1,00 lb, 0,16 - 0,45 kg |
| Groß | Schwere Strukturen:Pumpen, Kompressoren, Schweißkonstruktionen, Laufräder, Gebäudefundamente und andere sehr große Strukturen | > 1,00k lbf, pk, > 4,44k N pk | < 5 mV / lbf, <1,10 mV / N | > 1.00 lb, > 0,45 kg |
Nach Auswahl der am besten geeigneten Hammergröße, sollten weitere Eigenschaften des Hammers berücksichtigt werden:
Frequenzgang – Frequenzbereich, Auswahl der optimalen Schlagspitze
Hammergröße und -gewicht – praktische Überlegungen
Messbereich – Gewährleistung einer ausreichenden Schlagkraft
Empfindlichkeit – Vermeidung von Übersteuerung und nicht ausreichenden Signalstärken
Nichtlinearität - Konsistenz und Genauigkeit
Hammer Spitze
Wenn es um den Frequenzbereich für den Modaltest geht, ist die Wahl der richtigen Hammerspitze wichtig. Ein härteres Spitzenmaterial bietet einen größeren Frequenzbereich, kann es aber auch schwieriger machen, Doppelschläge zu vermeiden. Eine weichere Hammerspitze liefert eine längere Schlagzeit und folglich eine bessere Energieübertragung auf die Struktur bei niedrigeren Frequenzen, andererseits verringert sich allerdings die Frequenzspanne im Modaltest.
Als Faustregel sollte ein Hammerspitzenmaterial mit einem Frequenzgang gewählt werden, bei dem die Dämpfung bei der oberen Modaltestfrequenz unter 6 dB beträgt
Was ist ein Modalshaker?
Modalshaker sind Schwingungsanreger, die zur Anregung großer oder komplexer Strukturen und zum Erhalt hochwertiger Modaldaten verwendet werden. Im Vergleich zu Modalhämmern können Modalshaker die Struktur in einem breiteren Frequenzbereich und mit vielen verschiedenen Signalarten anregen, wodurch sie bestens für unterschiedliche Strukturen geeignet und ideal für genaue Testergebnisse sind.
Außerdem lassen sich Modalshaker so steuern, dass die Strukturen mit bestimmten benutzerdefinierten Anregungsamplituden angeregt werden, die dazu genutzt werden können, eine lineare oder der jeweiligen Anwendung entsprechend geformte Übertragungskurve zu erzielen. Durch die Steuerung der Anregungsamplitude des Shakers kann die Struktur vor kritisch hohen Amplitudenausschlägen geschützt werden, und es können verschiedene Amplituden getestet werden, um zu analysieren, wann nicht-lineare Effekte auftreten.
Es können mehrere Shaker zusammen mit und ohne kontrollierte Amplituden- und/oder Phasenmuster verwendet werden. Die Verwendung mehrerer Shaker an komplexen Strukturen ermöglicht eine realistischere Kraftanregung und eine bessere Untersuchung aller Eigenformen.
Arten von Schwingungsanregern für Modaltests
Hier die wichtigsten Arten von Schwinganregern für Modaltests (Shakern)
Permanentmagnet Shaker
Modal-Shaker
Inertial-Shaker
Als Modalshaker können verschiedene Typen von Schwinganregern eingesetzt werden, wobei jeder Typ seine Vor- und Nachteile hat, z. B. hinsichtlich des maximalen Anregungskraftpegels, des Frequenzbereichs und nicht zuletzt der Befestigungsweise des Shakers am Prüfling.
Permanent Magnet Shakers
Ein „normaler“ Schwinganreger oder Permanentmagnet-Shaker ist ein für allgemeine Zwecke geeigneter Shaker, an dessen Anker der Prüfling direkt befestigt und die schwingende Fläche durch Verwendung eines Kopfexpanders entsprechend den Probengrößen vergrößert werden kann.
Shaker dieses Typs werden üblicherweise eingesetzt für:
Schwingungstests an Mikroteilen und Modaltests an Baugruppen und Elektronik
Schockprüfungen
Sensorkalibrierung
Ermüdungsprüfungen und Resonanztests
Bildungs- und Forschungszwecke
Modalshaker
Modalshaker (oder Modalanreger) bieten im Vergleich zu normalen Schwinganregern einige Vorteile für die Durchführung von Modaltests.
Anstatt den Prüfling am Anker des Shakers zu befestigen, wird ein Modalshaker über einen Verbindungsstab (den sogenannten „Stinger“) mit dem Prüfling verbunden.
Modalshaker sind mit einer Armatur mit durchgehender Bohrung ausgestattet, so dass der Stinger, ohne den Shaker zu bewegen, auf die für den Prüfling erforderliche Länge angepasst werden kann, was das Setup vereinfacht.
Modalshaker werden üblicherweise verwendet für:
elektronische Baugruppen
Teilkomponenten
Maschinen
Fahrzeuge
Flugzeuge und Bauwerke
Je nach ausgewähltem Typ weisen Modalshaker unterschiedliche Spezifikationen auf. Üblicherweise können sie für die unten genannten Bereiche gewählt werden:
| Ausgangskraft | Frequenzbereich | Auslenkung pk-pk |
|---|---|---|
| ~ 20 N, 4.5 lbf - 500 N, 112 lbf | ~ 0 Hz - 12 kHz | ~ 5mm, 0.2 inch - 25 mm, 1 inch |
Der "Stinger" ist ein dünner flexibler Stab, der die Genauigkeit des Modaltests verbessert, indem er Kraft hauptsächlich in axialer Richtung auf den Kraftsensor oder Impedanzkopf überträgt. Die laterale Flexibilität schützt außerdem sowohl den Prüfling als auch den Modalshaker vor kritischen Kräften.
Intertial-Shaker
Intertial-Shaker werden für Strukturen verwendet, die eine Anregung in niedrigeren Frequenzbändern erfordern. Diese Shaker werden direkt mit der Struktur verbunden, und die auf die Struktur einwirkende Kraft wird durch die Massenträgheit der Shaker erzeugt.
Intertial-Shaker eignen sich grundsätzlich für die gleichen Anwendungsbereiche wie Modalshaker: Modaltests und eine Vielzahl allgemeiner Schwingungstestanwendungen. Abhängig von den Abmessungen der Struktur und den für die Schwingungstests erforderlichen Anregungsfrequenzen und -amplituden kann eine Wahl zwischen Modal- und Intertial-Shakern getroffen werden.
Je nach ausgewähltem Typ weisen Intertial-Shaker unterschiedliche Spezifikationen auf. Üblicherweise können sie für die unten genannten Bereiche gewählt werden:
| Ausgangskraft | Frequenzbereich | Gesamtmasse des Shakers |
|---|---|---|
| ~ 5 N, 1.1 lbf - 40 N, 9 lbf | ~ 10 Hz - 3 kHz | ~ 0.05 kg 0.11 lb - 0.5 kg, 1.1 lb |
Weitere Infos dazu:

Shaker-Anregungssignale
Wir unterscheiden folgende Signalformen für die Anregung der Shaker:
Zufallssignal
Burst-Zufallssignal
Pseudozufallssignal
Periodisches Zufallssignal
Sinus-Chirp
Gleitsinus und Stufensinus
Zufallssignal
Die Zufallsanregung (oder reine Zufallsanregung) liefert ein „weißes Rauschen“ mit zufälliger Amplituden- und Phasenvariation innerhalb eines definierten Frequenzbereichs. Bei der Zufallsanregung ist ein Leck-Effekt (Leakage) bei den Spektralschätzungen unvermeidbar, da das stochastische Signal nicht periodisch ist. Der Leck-Effekt lässt sich bis zu einem gewissen Grad durch die Verwendung eines Zeitbewertungsfensters (z. B. Hanning-Fenster) und die Erhöhung der spektralen Auflösung (Verringerung des Spektrallinienabstands Δf) handhaben.
Die Zufallsanregung bietet einen recht guten Crest- oder Scheitelfaktor (Verhältnis von Scheitelwert zu Effektivwert) und ein gutes Signal-Rausch-Verhältnis und zählt (sofern eine Mittelung durchgeführt wird) zu den besten Signalarten für die lineare Näherung eines Systems im Fall von Nichtlinearitäten. Durch die erforderliche Mittelung verlängert sich allerdings die Testzeit.
Burst-Zufallssignal
Im Gegensatz zu rein zufälligen Anregungssignalen tritt beim Burst-Zufallssignal bei richtiger Wahl der Burstrate kein Leck-Effekt auf. In einem solchen Fall kann ein einheitliches Fenster verwendet (oder auf ein Fenster verzichtet) werden. Der Burst-Random-Anregungstyp ist eine relativ schnell zielführende Signalart; im Vergleich zu rein stochastischen Anregungen ist der Scheitelfaktor allerdings höher und das Signal-Rausch-Verhältnis geringer.
Pseudozufallssignal
Die pseudostochastische Anregung ist schnell und leakage-frei und bietet sowohl einen recht guten Scheitelfaktor als auch ein recht gutes Signal-Rausch-Verhältnis. Allerdings kann ein Pseudozufallssignal nicht zur linearen Näherung eines nichtlinearen Systems verwendet werden.
Bei pseudostochastischen Anregungssignalen wird der gleiche Block eines zufälligen Zeitsignals in einer Schleife wiederholt. Dadurch schwingt sich die getestete Struktur auf eine periodische Antwort ein, und durch die Verwendung eines rechteckigen Bewertungsfensters lassen sich leakage-freie Messungen erreichen.
Pseudozufallssignale sind ergodische stationäre Signale (Quelle 7.1), die so gewählt werden, dass sie eine sich wiederholende Zeitblocklänge haben, die mit der verwendeten FFT-Zeitblocklänge (T) übereinstimmt, und nur aus Energieinhalten in ganzzahligen Vielfachen der FFT-Frequenzlinien (Δf) bestehen.
Bei pseudostochastischen Signalen ist der Energieinhalt der Spektralkomponenten festgelegt, haben aber zufällige Phasen. Der feste Energieinhalt der Spektralkomponenten kann über den verwendeten Frequenzbereich konstant sein oder aber gewichtet, um die Energie im Bereich der Resonanzen zu konzentrieren.
Periodisches Zufallssignal
Periodische Zufallssignale sind eine Kombination aus reinen und Pseudozufallssignalen, die die Vorteile leakage-freier Messungen und der besten linearen Näherung eines Systems bietet. Allerdings ist die Testzeit länger als bei Verwendung stochastischer oder pseudostochastischer Anregungssignale.
Ein periodisch stochastisches Signal ist ein Pseudozufallssignal, das sich über die Zeit ändert – wenn ein Pseudozufallssignal einige FFT-Zeitblöcke (T) lang gelaufen ist, verändert es sich in ein anderes Pseudozufallssignal. Dieser Prozess wird über die gesamten Modalmessungen hinweg fortgesetzt.
Dadurch hat die Struktur Zeit, sich auf die durch die verschiedenen Pseudozufallssignale hervorgerufenen stationären Antworten einzuschwingen. Für die Modalanalyse wird nur der letzte Zeitblock jedes Pseudozufallssignals (nach Einschwingen der Struktur) verwendet.
Beim periodischen Zufallssignal handelt es sich wie beim pseudostochastischen Signalen ebenfalls um ein ergodisches, stationäres Zufallssignal (Quelle 7.1), das nur aus Energie in ganzzahligen Vielfachen des FFT-Frequenzinkrements besteht.
Bei periodischen Zufallssignalen weist der spektrale Inhalt jedoch sowohl eine zufällige Amplituden- als auch eine zufällige Phasenverteilung auf.
Sinus-Chirp
Bei einem Chirp-Signal durchläuft ein Sinus-Sweep über jeden FFT-Zeitblock T einen definierten Frequenzbereich. Chirp-Signale fallen in die gleiche Kategorie wie pseudostochastische Signale und haben die gleichen nützlichen Eigenschaften und Nachteile. Allerdings ist bei Sinus-Chirps der Scheitelfaktor auf unter 2 reduziert und das Signal-Rausch-Verhältnis hoch, und das Spektrum ist linear und hat eine kontinuierliche Phase. Chirp-Signale sind gut zur Messung von Nichtlinearitäten in Strukturen geeignet.
Gleitsinus (Swept Sine) und Stufensinus (Stepped Sine)
Gleitsinus- und Stufensinus-Anregungen haben die gleichen Signalcharakteristika wie Chirp-Signale, es wird aber nicht in jedem FFT-Zeitblock T der gesamte Frequenzbereich durchlaufen. Stattdessen wird jeweils nur ein kleinerer Teil des Frequenzbereichs erfasst, und die endgültigen Vollbereichsmessungen setzen sich aus einer Reihe getrennt erfasster Frequenzkomponenten zusammen.
Wie die Chirps-Anregung eignen sich Gleitsinus- und Stufensinus-Anregungen gut zur Untersuchung von Nichtlinearitäten in Strukturen, und mit der benutzerdefinierten Sweep- oder Step-Rate lassen sich bestimmte Frequenzen und Moden einfach und detailliert analysieren.
Beim Stufensinus hat die Struktur Zeit, sich auf eine stationäre Antwort einzuschwingen, bevor Daten für eine bestimmte Frequenz extrahiert werden. Nach der Datenextraktion springt das Signal zur nächsten Frequenz, und die Struktur schwingt sich erneut ein. Dieser Prozess wird über den gesamten Frequenzbereich fortgesetzt.
Die Amplitude kann bei den verschiedenen Step-Frequenzen gesteuert werden. Werden mehrere Modalshaker und damit mehrere Anregungssignale gleichzeitig verwendet, dann wird auch ihr Phasenmuster gesteuert.
Bei vielen Softwareanwendungen wird für Gleitsinus und Stufensinus ein dynamisches Resampling verwendet, bei dem der FFT-Zeitblock eine dynamische, von der Sinusfrequenz abhängige Dauer hat. Anstelle eines festen Wertes T wird für die FFT-Zeitblockgröße eine dynamische Zeit definiert, die einer bestimmten Anzahl von Sinusperioden entspricht.
Modaltest-Ergebnisse
FRF (Frequenzgangfunktion)
Das primäre Ergebnis, das aus experimentellen Modaltests zu extrahieren ist, sind die Frequenzgangfunktionen (FRF) zwischen den Referenz-DOF und allen DOF des geometrischen Modells.
FRF sind Maße für das Verhältnis zwischen Antwortbewegung und Anregungskraft und beschreiben damit die inhärenten Eigenschaften eines linearen Systems.
Für jede FFT-Frequenzkomponente werden FRF-Werte berechnet – so ergeben sich Frequenzgangfunktionen über den gesamten gemessenen Frequenzbereich.
Der Betrag einer FRF wird oft in den Einheiten [m/s^2 / N] oder [g / lbf] angegeben. Bei Frequenzen mit hohen FRF-Betragswerten ist die Struktur empfindlicher und die Ausgangsantwort auch bei niedrigeren Eingangskraftpegeln relativ hoch. Liegt der FRF-Betrag auf einem lokalen Maximum/Peak und dreht sich die Phase an diesem Punkt um 90 Grad, dann weist dies in der Regel auf eine Resonanz hin. Dies kann durch eine Prüfung der Kohärenz bestätigt werden.
Umgekehrt ist die Struktur bei Frequenzen mit niedrigen FRF-Betragswerten unempfindlicher gegen einwirkende Kräfte und die Ausgangsantwort auch bei höheren Eingangskraftpegeln relativ gering. Täler zeigen oft Antiresonanzfrequenzen der Struktur an.
Hochwertige FRF-Daten aus genauen Modaltests sind eine Voraussetzung für erfolgreiche Modalanalysen, da Modalmodelle mit Eigenfrequenzen, Dämpfung und Eigenformen auf FRF-Daten basieren.
Die besten Methoden für den Erhalt qualitativ hochwertiger FRF-Daten sind:
Minimierung von Leck-Effekten durch Verwendung einer relativ hohen Frequenzauflösung. Dies kann durch Vergrößerung der FFT-Zeitblocklänge T erreicht werden, da der FFT-Linienabstand .
Minimierung des Rauschens bei den Eingangs- und Ausgangssignalen (wenn möglich)
Mittelung zur Minimierung unkorrelierter Rauschfehler. Bei stärkerem Rauschen ist eine höhere Anzahl zu mittelnder Werte erforderlich. Da die Rauschamplituden von Anwendung zu Anwendung variieren, unterscheidet sich auch die optimale Anzahl der zu mittelnden Werte. Als Faustregel gilt, dass bei Shaker-Tests 32–64 Messwerte und bei Impulshammertests 4–8 Messwerte gemittelt werden sollten.
Weitere Infos dazu:

FRF-Formulierung
Bei zwei Signalen und als Eingangs- bzw. Ausgangssignal kann die FRF aus der Gleichung
abgeleitet werden, wobei und komplexe Spektren von und sind. Weitere Informationen über Spektren sind im Anhang zu finden
FRF
Die - Variante der FRF minimiert den Fehler im Ergebnis bei einem verrauschten Ausgangssignal. FRF ist der beste Schätzer bei Antiresonanztälern der -Funktion:
und für MIMO:
Siehe auch hier den Anhang für die Formulierung von und , und 2x2 MIMO FRF H1.
FRF
Die -Variante der FRF minimiert den Fehler im Ergebnis bei einem verrauschten Eingangssignal. FRF ist der beste Schätzer bei Resonanzspitzen der H-Funktion:
und für MIMO:
Beachten Sie, dass für das Ausgangssignal b konjugiert wird.
ODS-Ergebnisse (Betriebsschwingform)
Die aus der ODS resultierenden Schwingformen werden in Form animierter geometrischer Modelle und der ermittelten Antwortamplituden- und Phaseninformationen angezeigt – und liefern hierbei die Schwingungsmuster des Prüflings.
Die Antwortamplituden werden manchmal in den Einheiten der Beschleunigung, Geschwindigkeit und Weg angegeben, jeweils berechnet anhand der absoluten skalierten Antwortmessung (z. B. aus den Autospektren der einzelnen DOF bei der Durchführung der Spektral-ODS).
Die Phaseninformation wird zwischen der/den Referenz-DOF und allen DOF extrahiert, z. B. aus den Kreuzspektren oder den Kreuzleistungsdichtespektren (CPSD) bei Durchführung der Spektral-ODS.
Beachten Sie, dass Betriebsschwingformen für alle Frequenzkomponenten bestimmt werden können, während Eigenformen aus EMA-Tests nur für die Eigenfrequenzen definiert sind. Eine Betriebsschwingform in der Nähe einer einzelnen Eigenfrequenz wird von der Eigenform bei dieser Frequenz dominiert.
Wenn die Eigenformen eines Prüflings klar voneinander getrennt sind und sich nur geringfügig überlappen, können ODS-Tests ähnliche Schwingformen ergeben wie die anhand der EMA kalkulierten Eigenformen.
Modaltest-Validierung
Kohärenz
Kohärenzdaten liefern wichtige Informationen für die Validierung von Modaltests. Die Kohärenz zeigt an, wie ein DOF oder eine Gruppe von DOF mit einem anderen DOF korreliert ist. Für jede FFT-Frequenzkomponente wird ein Kohärenzwert berechnet – so ergeben sich Kohärenzfunktionen über den gesamten gemessenen Frequenzbereich.
Kohärenzfunktionen werden während eines Modaltests üblicherweise zu Qualitätskontrollzwecken überwacht.
Gewöhnliche Kohärenz
Gewöhnliche Kohärenz (oder einfach „Kohärenz“) ist ein Kohärenzmaß zwischen zwei DOF.
Die gewöhnliche Kohärenz kommt bei Einzel-Referenz- und Multi-Referenz-Modaltests zum Einsatz, sollte bei Multi-Referenz-Modaltests aber nur zwischen Referenz-DOF verwendet werden.
Einzel-Referenz-Modaltests:
Validierung der Korrelation zwischen einem einzelnen Referenz-DOF und anderen einzelnen DOF
Die Kohärenz zwischen einem Referenz-DOF und anderen einzelnen DOF sollte immer hoch sein (nahe dem Wert 1), denn eine gute Übereinstimmung von Ausgangs- und Eingangssignal – möglichst ohne Einwirkung anderer Störsignale – ist für eine aussagekräftige Messung unerlässlich. Ist der Kohärenzwert bei einigen Frequenzen niedrig, dann sind die Modaldaten ungenau und können bei diesen Frequenzen ungültig sein. Andererseits sind niedrige Werte bei Antiresonanzfrequenzen und niederfrequenten Starrkörperschwingungen akzeptabel.
Allgemein können niedrige Kohärenzwerte aufgrund von Rauschen und Leck-Effekten in den Messungen auftreten, oder z. B. wenn sich das Testobjekt zeitvariant verhält oder Nichtlinearitäten vorliegen.
Multi-Referenz-Modaltests:
Validierung der Korrelation zwischen zwei Referenz-DOF, z. B. bei Verwendung mehrerer Schwingungsquellen
Der Kohärenzwert zwischen zwei Referenz-DOF, z. B. bei MIMO-Test mit mehreren Shakern, sollte niedrig sein (nahe 0), da vollkommen unkorrelierte Referenzsignale erwünscht sind. Nur wenn die Referenzsignale unkorreliert sind, ist es möglich, zwischen den Referenz-DOF zu unterscheiden und gültige MIMO-FRF und andere Modaldaten zu berechnen.
Eine gewöhnliche Kohärenz zwischen zwei Signalen und ist definiert durch die Gleichung
für die gilt:
wobei ein Wert von 1 eine perfekt lineare Beziehung zwischen den beiden Signalen signalisiert und ein Wert von 0, dass sie nicht zueinander in Korrelation stehen.
Die Kohärenz ist nur bei einer Mittelung über viele Datenblöcke gültig. Ohne Mittelung ist gleich 1.
Multiple Kohärenz
Multiple Kohärenz ist die Kohärenz zwischen einer Gruppe von Referenz-DOF und einem anderen DOF.
Die multiple Kohärenz kommt nur bei Multi-Referenz-Modaltests zum Einsatz.
Die multiple Kohärenz zwischen einem Referenz-DOF und anderen einzelnen DOF sollte immer hoch sein (nahe dem Wert 1), da es erwünscht ist, eine bestmögliche Übereinstimmung von Ausgangs- und Eingangsenergie – unabhängig von allfälligen Störsignalen – zu erzielen. Auch hier gilt: Ist der Kohärenzwert bei einigen Frequenzen niedrig, dann sind die Modaldaten ungenau und können bei diesen Frequenzen ungültig sein (außer bei Starrkörperschwingungen und Antiresonanzen).
Multiple Kohärenz ist ein Maß für die lineare Beziehung zwischen einer Signalgruppe und einem Signal . Die multiple Kohärenz ist definiert durch die Gleichung:
für die gilt:
wobei ein Wert von 1 eine lineare Beziehung zwischen allen Signale in der ausgewählten Gruppe und dem Signal signalisiert und ein Wert von 0, dass keines der Signale in einer Korrelation zu steht.
Modalanalyse
Der nächste Schritt nach der Erfassung der Modaltestdaten ist die Identifizierung der modalen Parameter mithilfe von Parameterschätzungsmethoden, einschließlich Mode Indicator Functions (MIF) und Kurvenanpassern.
Schätzung der modalen Parameter
Eigenfrequenz-Indikator-Funktionen (Mode Indicator Functions, MIF)
Eigenfrequenz-Indikator-Funktionen helfen, zu bestimmen, wie viele modale Eigenformen in den Modaltestdaten vorhanden sind. Es kann schwierig sein, dies auf der Grundlage nur einer FRF zu ermitteln, da einige Moden z. B. richtungsabhängig sein können und dadurch nicht in allen FRF zu beobachten.
Zur Unterstützung des Modenauswahlprozesses wurden verschiedene Arten von MIF entwickelt, die alle ihre spezifischen Verwendungszwecke haben. Einige von ihnen werden im Folgenden beschrieben.
PMIF (Power Mode Indicator Function)
NMIF (Normal Mode Indicator Function)
CMIF (Complex Mode Indicator Function)
PMIF (Power Mode Indicator Function)
Die Power Mode Indicator Function oder PMIF (auch Summenfunktion oder SUM) summiert eine Gruppe von Übertragungsfunktionen oder alle Übertragungsfunktionen. Die PMIF zeigt Peaks bei Moden des Prüflings, und bei Einbeziehung aller FRF können alle Moden der gemessenen Struktur angezeigt werden.
Die PMIF veranschaulicht die Moden recht gut, vor allem, wenn sie klar voneinander getrennt sind.
Die PMIF ist definiert durch:
NMIF (Normal Mode Indicator Function)
Mit Normal Mode Indicator Functions oder NMIF (auch Ordinary Mode Indicator Functions oder Original Mode Indicator Functions) lassen sich eng benachbarte Moden besser identifizieren als mit PMIF.
Die Formulierung von NMIF umfasst den Realteil der FRF, der bei einer Resonanz steilflankig durch Null geht und daher besseren Aufschluss über individuelle Moden gibt als PMIF.
Die NMIF hat Werte im Intervall [0, 1], wobei die Eigenformen auf der Kurve durch Peaks angezeigt werden.
Die NMIF ist definiert durch:
CMIF (Complex Mode Indicator Function)
Complex Mode Indicator Functions oder CMIF haben eine Funktion für jeden enthaltenen Referenz-DOF (Polyreferenz) und sind in der Lage, eng benachbarte Moden mit Repeated Roots zu erkennen.
CMIF basiert auf einer Singulärwertzerlegung (SVD) der FRF zur Identifikation aller bei den Modaltestmessungen erfassten Moden.
Die CMIF-Funktionen zeigen Peaks bei Resonanzen und weisen so auf Pole des Prüflings hin.
Kurvenanpassung (Curve Fitting)
Die Kurvenanpassung ist der Hauptprozess der Modalparameterschätzung, bei dem die Modalparameter – Eigenfrequenzen, Dämpfungskoeffizienten und Eigenformen – aus den gemessenen Modaltestdaten extrahiert werden. Dies geschieht durch Kurvenanpassung an die Modalmessungen und Extraktion der Parameter aus der ermittelten analytischen Darstellung der Daten.
Um gültige und möglichst genaue Modalschätzungen zu erhalten, sind bei der Durchführung der Kurvenanpassung diverse Aspekte zu berücksichtigen, die sich folgendermaßen klassifizieren lassen:
einer oder mehrere Freiheitsgrade (SDOF oder MDOF)
einer oder mehrere DOF (lokale oder globale Anpassung)
eine oder mehrere Referenzen (Monoreferenz oder Polyreferenz)
Einfreiheitsgrad-Verfahren (Single Degree of Freedom, SDOF)
Die SDOF-Kurvenanpassung kann bei einfachen Strukturen mit klar voneinander getrennten Moden mit nur geringen Überlappungen eingesetzt werden sowie in eingeschränkten Frequenzbändern, in denen diese Anforderungen erfüllt sind.
In vielen Fällen sind Strukturen schwach gedämpft (<1 %), was auch oft dazu führt, dass die Moden kleine Überlappungen haben; solche Moden werden als „schwach gekoppelt“ bezeichnet.
Mehrfreiheitsgrad-Verfahren (Multi Degree of Freedom, MDOF)
Die MDOF-Anpassung sollte bei Strukturen mit eng benachbarten Moden und bei stark gedämpften und sich dadurch überlappenden Moden verwendet werden. Auch MDOF ist nur für eingeschränkte Frequenzbereiche geeignet, in denen solche Eigenschaften gegeben sind.
Globale Anpassung
Die globale Kurvenanpassung basiert auf Daten mehrerer DOF. Durch die Verwendung von FRF-Datensets aus mehreren DOF lassen sich die globalen modalen Parameter (Frequenz und Dämpfung) oft besser bestimmen als durch lokale Kurvenanpassung. Das liegt daran, dass einige Moden möglicherweise bei einzelnen FRF-Messungen, aber nicht bei allen verwendeten FRF nachweisbar sind.
Bei der Durchführung einer globalen Kurvenanpassung müssen alle verwendeten Messungen globale Moden enthalten. Andernfalls könne die Ergebnisse ungenau werden.
Lokale Anpassung
Die lokale Kurvenanpassung basiert auf einzelnen (oder einer kleineren Gruppe von) realen FRF-Messungen. Solche Schätzer können bei der Analyse lokaler Moden des Prüflings verwendet werden.
Sind alle Moden global, dann sollte man auf einen globalen Kurvenanpasser zurückgreifen.
Monoreferenz-Anpassung
Die Monoreferenz-Kurvenanpassung basiert auf Modaltest-Messungen mit einem einzelnen Referenz-DOF. Bei diesem einzelnen Referenz-DOF kann es sich um einen Anregungs-DOF (z. B. bei einem Test mit ortsfestem Shaker oder einem Impact-Test mit wanderndem Beschleunigungssensor) oder um einen Antwort-DOF (z. B. bei einem Test mit wanderndem Hammer) handeln.
Polyreferenz-Anpassung
Die Polyreferenz-Kurvenanpassung basiert auf Modaltest-Messungen mit mehreren Referenz-DOF, wie z. B. bei einem Multi-Shaker-MIMO-Tes oder einem Test mit wanderndem Hammer und mehreren Referenz-Antwort-DOF.
Die Polyreferenz-Kurvenanpassung ist in der Lage, eng benachbarte Moden mit Repeated Roots zu trennen. Solche Moden können z. B. bei der Messung eines Prüflings mit einigen symmetrischen Maßen auftreten. In solchen Fällen ist es möglich, dass mehrere Moden die gleiche Resonanzfrequenz haben und sich ein Peak dadurch auf mehrere Moden bezieht.
Kurvenanpassungsverfahren
Der Hauptzweck der Kurvenanpassung besteht darin, die Modaldaten mathematisch bestmöglich darzustellen. Zu diesem Zweck wurden viele verschiedene Arten von Kurvenanpassungsalgorithmen entwickelt, von denen einige Zeitbereichs- und andere Frequenzbereichsdaten verwenden.
Die auf Zeitreihen basierenden Anpassungsalgorithmen verwenden Impulsantwortfunktionen (IRF) für die Parameterschätzung, während frequenzbasierte Algorithmen auf FRF zurückgreifen.
Sie alle haben ihre Vor- und Nachteile, z. B. in Bezug auf die Strukturdynamik (einfaches oder komplexes Testobjekt) oder die Anzahl der Moden für die Anpassung (Anpassungen hoher oder niederer Ordnung).
In der nachstehenden Tabelle sind verschiedene häufig verwendete Kurvenanpassungsverfahren mit ihrem Verarbeitungsbereich (Zeit oder Frequenz) und der am besten passenden Modellordnung (hohe oder niedere Ordnung) aufgeführt:
| Kurvenanpassungsmethode | Zeitbereich | Frequenzbereich |
|---|---|---|
| Low Order Fitting | ITD MRITD ERA | PFD-1 PFD-2 PFD-Z SFD MRFD |
| High Order Fitting | CEA LSCE PTD | RFP OP PLSCF RFP-Z PolyMAX AF-Poly |
Häufig wird die Kurvenanpassung im Zeitbereich für schwach gedämpfte Strukturen und die Kurvenanpassung im Frequenzbereich für stark gedämpfte Strukturen gewählt.
Einer der wichtigsten Parameter für die Kurvenanpassung ist die Ordnung (auch Iteration oder modale Größe), die die polynomiale Ordnung der angepassten mathematischen Funktion definiert.
Die Ordnung muss hoch genug für die Anpassung der Funktion an alle im ausgewählten Frequenzbereich/-band enthaltenen Moden und für die Kompensation der außerhalb des ausgewählten Kurvenanpassungsbandes liegenden Residueneffekte der Moden gewählt werden.
Andererseits darf sie aber auch nicht zu hoch gewählt werden, da die Anpassungsfunktion dann zusätzlich zu den Moden möglicherweise auch das Rauschen anpasst und physikalisch nicht interpretierbare rechnerische Moden auftreten.
Monoreferenz-Kurvenanpassung
MDOF LSCE, LSCF und RFP gehören zu den am häufigsten eingesetzten Kurvenanpassungsverfahren, da sie gut dazu geeignet sind, modale Parameter mit geringem Rechenaufwand genau zu berechnen, und recht deutliche Stabilitätsdiagramme liefern.
Für die Berechnung der Eigenformen wird häufig die LSFD-Approximierfunktion (Least-Squares Frequency Domain) verwendet. Als Grundlage dienen dabei die einzelnen, lokalen FRF-Datensets und die globalen Parameter wie Frequenz und Dämpfung.
Polyreferenz-Kurvenanpassung
Normale Monoreferenz-LSCF-Methoden sind nicht gut dafür geeignet, eng benachbarte Moden mit Repeated Roots zu trennen. Für solche Fälle wird stattdessen oft ein Polyreferenz-Kurvenschätzer verwendet. Polyreferenz-Kurvenanpasser sind z. B. pLSCF (oder PolyMax) und RFP-Z.
Schätzungsverfahren
Viele Verfahren zur Parameterschätzung passen die gemessenen Übertragungsfunktionen durch eine Polynomfunktion mit rationalem Bruch an, die auf folgendem Übertragungsfunktionsmodell mit gemeinsamem Nenner basiert:
wobei und für die Anzahl der gemessenen Ausgangs- bzw. Eingangskanäle stehen.
hier sind und die Nummern der gemessenen Ausgangs- bzw. Eingangskanäle.
Das Zählerpolynom für die -te Übertragungsfunktion ist definiert als:
wobei eine polynomische Basisfunktion und n der ausgewählten Polynommodellordnung ist. Die Polynomkoeffizienten sind die zu schätzenden Parameter, um die globalen Modalparameter zu schätzen.
Das gemeinsame Nenner-Polynommodell kann an die gemessenen Übertragungsfunktionen angepaßt werden, indem beispielsweise eine nichtlineare Kostenfunktion der kleinsten Quadrate (NLS) wie die unten gezeigte minimiert wird:
wobei die ausgewählte Gewichtungsfunktion ist. Nach Minimierung einer solchen Kostenfunktion werden die Pole und damit die globalen Frequenz- und Dämpfungsparameter aus den Wurzeln des Nennerpolynoms bestimmt.
Stabilitätsdiagramm
Ein Stabilitätsdiagramm (SD) hilft bei der Identifizierung stabiler Pole und damit konsistenter Moden. Die Pole enthalten Informationen über die Modalfrequenz und die Dämpfung. Bei einer Erhöhung der Ordnung der Schätzung erhöht sich auch die Anzahl der geschätzten Pole. Wenn sich diese Pole zwischen den einzelnen Nachbarordnungen nur noch wenig ändern, dann gelten sie als stabil – sie haben stabile Werte erreicht.
Modalanalyse-Anwendungssoftware bietet häufig die Option benutzerdefinierter Toleranzwerte, die dazu dienen, zu bestimmen, wann die Pole stabil sind. Solche Toleranzen können für die Frequenz und die Dämpfung oft einzeln festgelegt werden.
Von jeder Mode im Stabilitätsdiagramm wird ein stabiler Pol gewählt und dann zusammen mit den Residualdaten zur Berechnung der Eigenformen des Modalmodells verwendet.
Modellvalidierung
Der nächste Schritt nach Abschluss der Modalparameterschätzung ist die Validierung des Modalmodells. Die Validierung der modalen Parameter umfasst in der Regel z. B. MAC-Prüfungen und eine FRF-Synthese zum Vergleich mit den real gemessenen FRF-Daten.
Modal Assurance Criteria (MAC)
Die Analyse der Modal Assurance Criteria (MAC) wird zur Bestimmung der Ähnlichkeit zweier Eigenformen verwendet.
Der MAC-Wert ist als skalare Konstante zwischen 0 und 1 definiert, die den Grad der Übereinstimmung zwischen zwei Eigenformen ausdrückt.
In der Praxis gilt jeder Wert zwischen 0,9 und 1,0 als gute Korrelation und ein Wert unter 0,7 als Hinweis auf eine schlechte Korrelation.
AutoMAC
AutoMAC ist ein Verfahren, das zur Validierung der Genauigkeit von Modalmodellen verwendet werden kann.
Und es ist ein Maß für die Ähnlichkeit zwischen geschätzten Eigenformvektoren aus derselben Parameterschätzung mit demselben Datensatz.
Alle Diagonalwerte sind per Definition 1, da jede Eigenform perfekt mit sich selbst korreliert.
AutoMAC ist ein gutes Werkzeug, um zu bestimmen, welche und wie viele DOF in der Modalanalyse erforderlich sind, um räumliches Aliasing zu vermeiden. Bei räumlichem Aliasing sehen einige Moden aufgrund der unzureichenden Anzahl der bei den Messungen verwendeten DOF ähnlich aus. Werden nicht genügend DOF verwendet, dann reichen die erhaltenen Informationen nicht aus, um alle Modi getrennt zu beschreiben.
In einem AutoMAC-Diagramm erzeugt das räumliche Aliasing hohe Werte bei Elementen außerhalb der Diagonalen, was auf ein ähnliches Aussehen verschiedener Moden hinweist.
Wird ein ausreichend umfangreicher Satz von DOF in die Berechnungen einbezogen, dann können alle Modi gut unabhängig voneinander oder orthogonal zueinander sein. In solchen Fällen zeigt das AutoMAC-Diagramm einen Wert um 1 im Wesentlichen nur auf der Diagonalen, da jede Mode jeweils nur mit sich selbst korreliert.
AutoMAC ist definiert als:
wobei \{\Psi_r\}\) und {\Psi_s\} die modalen Vektoren für Modus \(r\) und Modus \(s\) sind.
CrossMAC
CrossMAC bestimmt die Übereinstimmung bzw. Linearität zwischen geschätzten Eigenformvektoren aus verschiedenen Schätzungen mit unterschiedlichen Datensätzen.
CrossMAC ist ein gutes Werkzeug zum Vergleich verschiedener experimentell ermittelter Eigenformen. Es kann zum Beispiel interessant sein, zwei Messreihen zu vergleichen, die unterschiedliche Referenz-DOF-Positionen verwenden, und die Übereinstimmung der Moden zwischen ihnen zu betrachten, oder zwei verschiedene Kurvenanpassungsalgorithmen zu vergleichen, die für dieselbe Messreihe verwendet wurden.
Außer zum Vergleich verschiedener experimentell ermittelter Eigenformen kann CrossMAC auch dazu dienen, einen Satz experimentell ermittelter Eigenformen mit einem Satz analytisch ermittelter Eigenformen aus einer Finite-Elemente-Analyse (FEA) zu vergleichen. Letztere wird zur Korrelationsanalyse verwendet.
CrossMAC ist definiert als:
wobei und unterschiedliche Schätzungen der Eigenform für denselben Modus sind.
Skalierung der Eigenformen
Im Gegensatz zu Residuen haben Eigenformen keinen eindeutigen Wert (sondern nur eine eindeutige Form) und können daher beliebig skaliert werden. Die Skalierung der Eigenform kann in vielerlei Weise stattfinden, für die EMA werden jedoch am häufigsten die folgenden drei Skalierungsmethoden verwendet:
Normalisierung der modalen Masse
Normalisierung der modalen Vektorlänge
Normalisierung der modalen Maximalkomponente
Wird die modale Masse auf eins normalisiert, dann wird die Skalierung der Eigenform als Einheitsmasse (UMM) bezeichnet.
Die modale Masse bezieht sich nicht auf die Masse des Prüflings, sondern ist eine mathematische Eigenschaft, für die ein beliebiger Wert außer gewählt werden kann. Die modale Masse wird zur Berechnung des Skalierungsfaktors verwendet.
Bei der Eigenformskalierung wird ein Skalierungsfaktor ar verwendet, der von der gewählten Skalierungsart abhängt.
Bei Verwendung der UMM-Skalierung wird die modale Masse auf gesetzt und der Skalierungsfaktor wird:
Die Fahrpunktreste werden zur Skalierung des modalen Modells verwendet, und es ist daher wichtig, gute und genaue Fahrpunktmessungen zu erhalten, die Informationen für alle Modi enthalten.
Dabei werden Eigenformvektoren aus dem Skalierungsfaktor ar und den treibenden Punktresten nach der Formel skaliert:
Bei der EMA wird häufig auf die UMM-Skalierung zurückgegriffen, da die aus den FRF erhaltenen Modaldaten keine Informationen über die Massenmatrix enthalten, die sonst zur Skalierung der Eigenformen verwendet werden könnten.
Residuen
Der lokale Modalresiduen-Parameter zwischen einem Anregungs-DOF DOF \(j\) und einem Antwort-DOF \(i\) bezieht sich die Amplitude der Eigenformen \(r\) und wird manchmal auch als „Polstärke“ oder „Modenstärke“ bezeichnet. Die Beziehung zwischen Residuen und Eigenformen wird beschrieben durch:
Bei MDOF-Modalparameter-Modellen gilt für die Beziehung zwischen den Residuen und den FRF in der Mobilitätsmatrix:
mit
FRF-Synthese
Die FRF-Synthese wird als Validierungswerkzeug verwendet, indem die Übertragungsfunktionen aus dem geschätzten Modalmodell (die synthetisierten FRF) mit den real gemessenen FRF-Daten verglichen werden. Hiermit lässt sich prüfen, wie gut das geschätzte Modell die Dynamik der physikalischen Struktur abbildet.
Zur Gewährleistung einer genauen FRF-Synthese ist eine Eigenformskalierung erforderlich.
Aus einem skalierten Modalmodell lassen sich dann in folgender Weise die auf die Eingangs- und Ausgangs-DOF bezogenen Übertragungsfunktionen synthetisieren:
Vergleich von ODS und OMA
Sowohl ODS als auch OMA verwenden keine externen Anregungskräfte, sondern basieren ausschließlich auf Messungen der Antwort-DOF. Dabei ist das Modaltestverfahren für ODS und OMA das gleiche, die Analyse und die Ergebnisse jedoch sind unterschiedlich.
Die ODS liefert grundlegende Informationen über Amplituden und Phasen der DOF am Prüfling unter Betriebsbedingungen und ermöglicht die Erstellung animierter geometrischer Modelle der Schwingformen.
Bei der OMA wird (wie bei der EMA) ein Modalmodell mit Eigenfrequenzen, Dämpfung und Eigenformen des unter Betriebsbedingungen gemessenen Prüflings geschätzt.
Während bei der EMA Modalmodelle anhand von FRF-Daten geschätzt werden, die durch Verwendung von Krafteingangssignalen erhalten wurden, greift die OMA zur Schätzung der Modalmodelle auf Betriebsschwingungsmessungen zurück und verwendet z. B. berechnete Auto- und Kreuzleistungsdichtespektrum-Funktionen (PSD und CPSD).
Da die OMA keine Eingangskraftsignale verwendet, sind die einwirkenden Kräfte unbekannt. Daher können keine Modalmassen geschätzt und die geschätzten Eigenformen nicht skaliert werden.
Die OMA kann zur Schätzung eines Modalmodells in Situationen verwendet werden, in denen es schwierig ist, eine EMA durchzuführen. Solche Situationen können sich z. B. bei der Zustandsüberwachung in Betrieb befindlicher Prüflinge ergeben, wenn die Größe oder der Standort des Prüflings eine externe Kraftanregung unmöglich macht oder wenn die im tatsächlichen Betrieb angeregten Schwingformen der Struktur analysiert werden müssen
Einleitung
Wie bereits zu Beginn dieses Artikels erwähnt, wird die Modalanalyse in verschiedenen industriellen Branchen in großem Umfang eingesetzt, um strukturdynamische Probleme bei Produkten zu untersuchen.
In vielen Fällen entstehen solche Probleme im Zusammenhang mit Produktoptimierungen wie z. B. Gewichtsreduzierung, Effizienzsteigerung oder Vereinfachung des Herstellungsprozesses, die sich negativ z. B. auf die Ermüdungslebensdauer, den Schwingungskomfort oder die Sicherheit auswirken können.
Über viele Jahre hinweg waren die meisten praktischen Anwendungen für die Modalanalyse in den Bereichen Luft- und Raumfahrt und Verteidigung, Automobilbau, Maschinenbau und Tiefbau zu finden, mit der rasanten Entwicklung neuer Technologien jedoch kommt sie immer mehr auch in allen möglichen anderen Bereichen und bei interdisziplinären Anwendungen zum Einsatz.
Nachfolgend finden Sie eine Liste typischer Anwendungsbereiche der Modalanalyse mit Angabe der für die jeweilige Anwendung am besten geeigneten Analysearten (EMA, ODS, OMA):
Automobil
Analyse von Fahrzeugrahmen (Rohkarosserie) – EMA
Pkw-Komponenten (z. B. Aufhängungen, Auspuffanlagen oder Bremsscheiben) – EMA
Motoren – EMA, ODS, OMA
Voll ausgestattete Pkw – EMA, ODS, OMA
Luft- und Raumfahrt und Verteidigung
Schwingungsanalyse an Flugzeugen mittels Ground-Vibration-Tests (GVT) – EMA
Flugzeugkomponenten (z. B. Fahrwerke oder Steuerflächen) – EMA
Motoren – EMA, ODS, OMA
Flugversuche (Flatterversuche) – ODS, OMA
Analyse von Trägerraketen (z. B. Nutzlasten, Nutzlastbefestigungen, Geräteträger oder Bordsysteme) – EMA, ODS, OMA
Bauwesen und zivile Industrie
Pumpen- und Kompressoranalyse – EMA, ODS, OMA
Maschinenzustandsüberwachung – ODS, OMA
Rohrleitungssysteme – EMA, ODS, OMA
Wellen und Lager – EMA, ODS, OMA
Windkraftanlagen – ODS, OMA
Turbinenschaufeln – EMA
Maschinenfundamente – ODS, OMA
Brücken, Dämme, Hochhäuser, Offshore-Plattformen – ODS, OMA
Audio- und Haushaltsgeräte
Waschmaschinen und ähnliche Haushalts-Großgeräte – EMA, ODS, OMA
Lautsprecher und Musikinstrumente – EMA, ODS, OMA
Automobil
Die Entwicklung von Kraftfahrzeugen umfasst eine sehr detaillierte Analyse z. B. der Strukturdynamik des Fahrzeugrahmens, die dazu beiträgt, eine hohe Sicherheit und einen guten Fahrkomfort zu gewährleisten. Ein Fahrzeugrahmen hat Resonanzfrequenzen, die vielleicht nur schwach gedämpft sind. Werden solche Resonanzfrequenzen während der Fahrt angeregt, dann kann es sehr wichtig sein, die dynamischen Eigenschaften des Rahmens so zu verändern, dass die strukturellen Resonanzen ausreichend gedämpft oder in einen nicht angeregten Frequenzbereich verschoben werden.
Die Modalanalyse erleichtert solche Veränderungsprozesse erheblich, indem sie die Auswirkungen der erwogenen Steifigkeits- und Dämpfungsmodifikationen am Fahrzeugrahmen untersucht und zum Beispiel zeigt, wie man das Gewicht des Rahmens reduzieren kann, ohne dessen Festigkeit zu beeinträchtigen.
Der Fahrzeugrahmen sollte nach der Modifikation kraftstoffeffizienter sein, aber trotzdem noch in der Lage, alle Crashtest-Szenarien erfolgreich zu überstehen.
Es wird für die Hersteller immer eine große Herausforderung bleiben, die Hauptparameter – wie Sicherheit, Komfort, Effizienz und Kosten – in ein Gleichgewicht zu bringen, und die Modalanalyse gehört zu den wichtigsten Werkzeuge zur Bestimmung und Optimierung dieses Gleichgewichts.
Geräusche in Fahrzeugen sind ein weiterer wichtiger Aspekt für die Automobilindustrie. Eine wesentliche Rolle spielen dabei der über die Fahrzeugkomponenten übertragene Körperschall und das Reifen-Fahrbahn-Geräusch. Die Übertragung solcher Geräusche in den Fahrzeuginnenraum kann mit Hilfe der Modalanalyse durch Messung der FRF-Funktionen der Luftschallübertragung untersucht werden. So kann sie einen wertvollen Überblick über die Zusammenhänge zwischen störenden Innenraumgeräuschen und spezifischen Fahrzeugkomponenten bieten.
Luft- und Raumfahrt und Verteidigung
In der Luft- und Raumfahrtindustrie wird die Modalanalyse schon seit vielen Jahren eingesetzt, da das Gewicht ein entscheidender Faktor für die Leistung von Flugzeugen und Raumfahrzeugen ist. Im Zusammenhang mit dem harten Wettbewerb in Bezug auf die Treibstoffeinsparung, der in der Branche herrscht, wird intensiv an der Entwicklung neuer leichter Materialien und Komponenten mit extremer Festigkeit gearbeitet.
Oftmals werden bei der Entwicklung dieser Komponenten Computersimulationsmodelle (FEM) benötigt, die verifiziert werden müssen. Die Modalanalyse ist eines der wichtigsten Werkzeuge zur Verifizierung solcher analytischen Modelle, da sie die Simulation glaubhafter „Was-wäre-wenn“-Szenarien erlaubt.
Die Verifizierung von Computermodellen ist in der Luft- und Raumfahrtindustrie besonders wichtig, da dort bei der Entwicklung optimierter Komponenten oft an die Grenzen der in den mathematischen Modellen verwendeten linearen Annahmen gegangen wird. Mittels nichtlinearer Modaltests lässt sich feststellen, wo diese Grenzen liegen. Zudem können solche Tests auch zeigen, wie sich manche nichtlineare Effekte auf die Strukturdynamik auswirken und unter welchen Bedingungen sich bei Simulationsmodellen Abweichungen von ähnlichen realen Szenarios ergeben.
So wie die Modalanalyse in der Automobilindustrie dazu einsetzt wird, Einblicke in die Ursachen der Innenraumgeräusche zu erhalten, kann sie bei U-Booten dazu dienen, zu ermitteln, wie sich bestimmte Geräuschmuster außerhalb des Fahrzeugs ausbreiten, und so zur Reduzierung der Geräuschspuren beitragen.
Die Modalanalyse kommt in vielen Bereichen der Raumfahrzeugentwicklung zum Einsatz, zu denen auch die Entwicklung von Startrampensystemen zählt. Zum Beispiel kann es von großem Interesse sein, zu untersuchen, wie die Startrampenstruktur, die das Raumfahrzeug bis zur Triebwerkszündung hält, schwingt, wenn sie durch Kräfte angeregt wird, die den bei einem echten Start auftretenden ähneln. Wenn die Techniker die Schwingungsmuster der Startrampenstruktur in das Startkontrollsystem integrieren, können realistischere Startsimulationen getestet werden.
Strukturdynamik – Brücken und Gebäude
Bei Bauwerken werden Modalanalysen dazu eingesetzt, die Auswirkungen von z. B. seismischen Aktivitäten oder starken Winden zu beurteilen. Dabei werden oft Output-only-Analysearten wie die OMA verwendet, bei denen die untersuchte Struktur ausschließlich durch Umgebungsschwingungen und externe Kräfte angeregt wird.
Bei hohen Wohngebäuden etwa könnten mittels einer Modalanalyse kritisch hohe Auslenkungswerte bei bestimmten Biege- oder Torsionsmoden nachgewiesen werden. Werden solche Moden erkannt, dann ist es oft möglich, Maßnahmen zu modellieren und zu implementieren, die diesen Eigenschaften entgegenwirken oder sie abschwächen.
Das Gleiche gilt für Brücken, bei denen bei bestimmten Windgeschwindigkeiten Flattereffekte auftreten können, die das Bauwerk in Schwingungen versetzen. Ein Beispiel für die möglichen fatalen Folgen dieses Effekts ist die Tacoma-Narrows-Brücke zwischen Tacoma und der Kitsap-Halbinsel im US-Bundesstaat Washington, die 1940 eröffnet wurde und nur vier Monate später durch Windeinwirkung einstürzte.
Weitere Infos:

Anhang – Zusätzliche Theorie
Kreuzspektrum
Mit zwei (komplexen) momentanen Spektren bzw. ist das Kreuzspektrum von und durch die Formel definiert:
Dementsprechend ist die Amplitude das Produkt der beiden Amplituden und die Phase ist die Differenz zwischen den beiden Phasen (von und )
Die einseitige Spektralform des Kreuzspektrums wird oft als bezeichnet und ist definiert durch:
MIMO 2x2 FRF - Formulierung
Mit zwei Eingangssignalen, und , und zwei Ausgangssignalen, und , kann FRF H1 abgeleitet werden durch
Wo
ist die transponierte Kofaktormatrix, wobei der Kofaktor von in it:
wobei die Nebenmatrix von ist.
Beachten Sie, dass jede Zeile der FRF-H1-Matrix nur von einem Ausgangssignal , aber von beiden Eingangssignalen abhängt.
wo
Beachten Sie erneut, dass jedes Antwortspektrum nur von einem Ausgangssignal b abhängt, aber von beiden Eingangssignalen .
Beachten Sie auch die Einheiten:
Wenn das Signal \(a(t)\) mit komplexem Spektrum \(A(f)\) die Einheit \(N\) (Force) hat, dann hat die Einheit und die Determinante \(det( G_{AA})\) hat die Einheit
Wenn das Signal mit komplexem Spektrum die Einheit (Acceleration) hat, dann hat die Einheit
In diesem Beispiel hat also jedes Element in der -Matrix die Einheit , was Sie sich als Antwort pro Erregung vorstellen können.
MIMO 2x2 Multiple Kohärenz - Formulierung
Wenn wir zwei Eingangssignale haben, und , und zwei Ausgangssignale, und , dann multiple Kohärenz für jedes Ausgangsantwortsignal oder (in Bezug auf die Gruppe der Eingangserregungen) kann abgeleitet werden durch:
wobei einen Vektor mit der Gruppe von Eingangssignalen darstellt und die konjugierte Transponierte (oder Hermitesche Transponierte) von ist.
wobei
Bezeichnungen für Kurvenanpassungsverfahren
| CEA | Complex Exponential Algorithm |
| LSCE | Least Squares Complex Exponential |
| PTD | Polyreference Time Domain |
| ITD | Ibrahim Time Domain |
| MRITD | Multireference Ibrahim Time Domain |
| ERA | Eigensystem Realization Algorithm |
| Polyreference Frequency Domain | |
| SFD | Simultaneous Frequency Domain |
| MRFD | Multireference Frequency Domain |
| RFP | Rational Fraction Polynomial |
| OP | Orthogonal Polynomial |
| PLSCF | Polyreference Least Squares Complex Frequency |
| REP-Z | Rational Fraction Polynomial-Z Domain |
Quellenangaben
Dewesoft
1.1. Modal Test - Pro-training
1.5. Order Tracking - Pro-training
Brüel & Kjær
2.1. APPLICATION NOTE: Modal Analysis using Multi-reference and Multiple-Input Multiple-Output Techniques by H. Herlufsen, Brüel & Kjær, Denmark,
2.2. Modal Hammer - Type 8210
2.3. APPLICATION NOTE: How to Determine the Modal Parameters of Simple Structures by Svend Gade, Henrik Herlufsen and Hans Konstantin-Hansen, Brüel & Kjær, Denmark
2.4. Structural Testing Part 2 - Modal Analysis and Simulation by Ole Døssing, Brüel & Kjær, Denmark
Crystal Instruments
3.1. Experimental Modal Analysis Overview
3.2. Basics of Modal Testing and Analysis
3.3. Modal Testing Excitation Considerations
3.4. Applications of Experimental Modal Analysis
The Modal Shop
4.1. Force Sensors and Impedance Heads
4.2. Modal Excitation Stingers for Modal Shaker Testing
Siemens
5.1. Modal Testing Guide
5.2. Using Pseudo-random for High-Quality FRF Measurements
5.3. OMG! What is OMA? Operational Modal Analysis
PCB Piezotronics
6.1. Modal Hammer Type 086c03
6.2. Modal Hammer Chart
Books
7.1. Random Data: Analysis and Measurement Procedures, by Julius S. Bendat and Allan G. Piersol, Edition 1 from 1971, chapter 1.2: Classification of Random Data.
7.2. Frequency Analysis - Brüel & Kjær, by R. B. Randall, B. Tech., B.A., 3rd edition from 1987, page 226 -252.
UMass Lowell - Modal Space Articles
8.1. What is the difference between all the mode indicator functions? by Pete Avitabile.
8.2. Curvefitting is so confusing to me! What do all the different techniques mean? by Pete Avitabile.
8.3. What's the difference between local and global curve fitting? by Pete Avitabile.
8.4. What effect can the test setup and rigid body modes have on the higher flexible modes of interest? by Pete Avitabile.
Other articles
9.1. Global Frequency & Damping Estimates From Frequency Response Measurements, by Mark H. Richardson Structural Measurement Systems, Inc. San Jose, California
9.2. The PolyMAX frequency-domain method: a new standard for modal parameter estimation?, by Bart Peeters, Herman Van der Auweraer, Patrick Guillaume and Jan Leuridan, LMS International, and Department of Mechanical Engineering at Vrije Universiteit Brussel
9.3. Spatial Information in Autonomous Modal Parameter Estimation, by Randall J. Allemang1 and Allyn W. Phillips, Department of Mechanical and Materials Engineering, College of Engineering and Applied Science, University of Cincinnati.
9.4. Frequency-Domain System Identification Techniques For Experimental And Operational Modal Analyses, By Patrick Guillaume, Peter Verboven, Bart Cauberghe, Steve Vanlanduit, Eli Parlor, and Gert De Sitter, Vrije Universiteit Brussel (VUB) Department of Mechanical Engineering Acoustics & Vibration Research.
9.5. Structural Dynamics Modeling using Modal Analysis: Applications, Trends, and Challenges, by Herman Van der Auweraer, LMS International
Wikipedia
10.1. Tacoma Narrows Bridge
