Inhaltsübersicht
Kategorien durchsuchen
Autoren durchsuchen
 AB
ABAlberto Boffi
 AL
ALAlessia Longo
 AH
AHAl Hoge
 AB
ABAljaž Blažun
 BJ
BJBernard Jerman
 BČ
BČBojan Čontala
 CF
CFCarsten Frederiksen
 CS
CSCarsten Stjernfelt
 DC
DCDaniel Colmenares
 DF
DFDino Florjančič
 EB
EBEmanuele Burgognoni
 EK
EKEva Kalšek
 FB
FBFranck Beranger
 GR
GRGabriele Ribichini
Glacier Chen
 GS
GSGrant Maloy Smith
 HB
HBHelmut Behmüller
 IB
IBIza Burnik
 JO
JOJaka Ogorevc
 JR
JRJake Rosenthal
 JS
JSJernej Sirk
 JM
JMJohn Miller
 KM
KMKarla Yera Morales
 KD
KDKayla Day
 KS
KSKonrad Schweiger
Leslie Wang
 LS
LSLoïc Siret
 LJ
LJLuka Jerman
 MB
MBMarco Behmer
 MR
MRMarco Ribichini
 ML
MLMatic Lebar
 MS
MSMatjaž Strniša
 ME
MEMatthew Engquist
 ME
MEMichael Elmerick
 NP
NPNicolas Phan
 OM
OMOwen Maginity
 PF
PFPatrick Fu
 PR
PRPrimož Rome
 RM
RMRok Mesar
 RS
RSRupert Schwarz
 SA
SASamuele Ardizio
 SK
SKSimon Kodrič
 SG
SGSøren Linnet Gjelstrup
 TH
THThorsten Hartleb
 TV
TVTirin Varghese
 UK
UKUrban Kuhar
Valentino Pagliara
 VS
VSVid Selič
 WK
WKWill Kooiker
Validierung des dynamischen Verhaltens einer einfeldrigen Stahl-Beton-Fußgängerbrücke

Im Rahmen einer Kooperation zwischen der Technischen Universität Krakau und Dewesoft Polen wurde das strukturelle Verhalten einer einfeldrigen Stahl-Beton-Verbundbrücke unter Fußgängerlasten untersucht. Die Untersuchung umfasste die dynamische Überwachung und die Verfeinerung eines mathematischen Modells zur Verbesserung von Simulationen. Zu den zentralen Phasen der Studie gehörten die Erstellung eines Finite-Elemente-Modells (FE), die Durchführung einer Betriebsmodalanalyse (OMA) und die Überprüfung der FE-Modellvorhersagen anhand von Feldtestdaten. Die Tests umfassten einen nutzerinduzierten Frequenzsweep sowie Belastungen durch Fußgänger, um die Eigenfrequenzen, Eigenformen und Dämpfungsverhältnisse der Brücke bei dynamischer Beanspruchung zu ermitteln.

Eines der bedeutendsten aktuellen Infrastrukturprojekte in Krakau ist die Łagiewnicka-Route, die als Teil der Südumgehung der Stadt eine effiziente Verkehrsverteilung ermöglichen soll. Bei dem Projekt handelt es sich um eine Reihe von Straßeninfrastrukturelementen mit einer Gesamtlänge von 3,5 km, von denen 2,1 km in Tunneln verlaufen. Der Raum oberhalb der Tunneltrasse ist für den lokalen Verkehr vorgesehen. Die Investition, deren Gesamtkosten sich auf rund 178 Mio. PLN (Polnische Złoty) belaufen, wurde mit Unterstützung von EU-Mitteln aus dem Operationellen Programm für Infrastruktur und Umwelt realisiert.
Das Projekt beinhaltet:
5,3 km neue Fußgängerwege
3,2 km neue Fahrradwege
3,1 km kombinierte Fußgänger- und Radwege
Ein zentrales Element des neuen Infrastruktursystems ist eine einfeldrige Stahl-Beton-Verbundfußgängerbrücke (siehe Abb. 1), die den Hauptverkehrsweg überspannt und Fußgängern eine sichere Querung ermöglicht.
Messkampagne
Die Zusammenarbeit zwischen dem Lehrstuhl für Struktur- und Materialmechanik an der Technischen Universität Krakau (CUT) und Dewesoft Polen begann im Juni 2024. Gemeinsam mit der auf Strukturdynamik spezialisierten Brückenbauingenieurin Dr. Izabela Drygala entwickelten wir ein Forschungsprogramm für die Fußgängerbrücke.
Die Untersuchung konzentrierte sich auf zwei Hauptthemen:
dynamische Überwachung der Struktur
Entwicklung eines mathematischen Masse-Feder-Dämpfer-Modells (MFD-Modell) zur Verbesserung numerischer Simulationen
Die beteiligte Brückenbauingenieurin Dr. Izabela Drygala sagt dazu:
Diese Daten sind entscheidend für das Verständnis der dynamischen Eigenschaften der Struktur – etwa ihrer Eigenfrequenzen, Dämpfungsverhältnisse und Eigenformen. Darüber hinaus bilden sie die Grundlage für die Kalibrierung und Validierung des mathematischen MFD-Modells, um sicherzustellen, dass die numerischen Simulationen das tatsächliche Verhalten der Struktur möglichst präzise abbilden.
Das mathematische MFD-Modell
Das mathematische MFD-Modell ist ein Rahmen zur Beschreibung und Analyse mechanischer Schwingungen in Systemen mit Masse-, Feder- und Dämpferelementen.
Dieses Modell ist in der Schwingungsanalyse und im Maschinenbau von grundlegender Bedeutung, da es das Verhalten schwingungsfähiger Systeme darstellt. Ingenieure verwenden es häufig in Anwendungen wie der Analyse von Fahrzeugaufhängungen, der Schwingungsregelung in mechanischen Systemen und der seismischen Analyse von Gebäudestrukturen.
Das Modell liefert Erkenntnisse darüber, wie Systeme auf verschiedene Kräfte reagieren, und unterstützt Ingenieure bei der Entwicklung von Systemen zur Schwingungskontrolle, Vibrationsminderung und Verbesserung der strukturellen Stabilität.
Komponenten des MFD-Modells
Masse (M): Repräsentiert die Trägheit des Objekts und wirkt Beschleunigungen und Verzögerungen entgegen.
Feder (F): Erzeugt eine Rückstellkraft, die proportional zur Auslenkung ist und dem Hooke’schen Gesetz folgt. Dabei bestimmt die Federkonstante k die Systemsteifigkeit.
Dämpfer (D): Repräsentiert ein Dämpfungselement, das eine zur Geschwindigkeit proportionale Widerstandskraft erzeugt. Diese Dämpfung wird in der Regel durch einen Koeffizienten c beschrieben, der angibt, wie schnell die Bewegung des Systems mit der Zeit abnimmt.
Die einfeldrige Fußgängerbrücke
Die einfeldrige Struktur mit einer Spannweite von 48 Metern zwischen den Auflagern besteht aus einem Stahlfachwerk, das mit einer 14–20 cm dicken Deckplatte verbunden ist. Die Stahlbauteile sind in Stahlgüte S355 ausgeführt, während die bewehrten Betonelemente der Festigkeitsklasse C30/37 verbundtechnisch mit der Stahlkonstruktion gekoppelt sind. Für strukturelle Details siehe Abb. 3 und 4.
Die Bauarbeiten endeten im Herbst 2021 mit den erfolgreich durchgeführten statischen und dynamischen Belastungstests. Im Sommer 2024 führten wir eine Versuchskampagne durch, um den Zustand des Bauwerks nach dreijähriger Nutzung zu bewerten. Wir entwickelten das Feldtestprogramm in enger Zusammenarbeit mit dem Betreiber und Verwalter des Bauwerks, der Trasa Łagiewnicka SA.
Die Feldtests konzentrierten sich auf die Bewertung des dynamischen Verhaltens der Fußgängerbrücke unter personeninduzierter dynamischer Belastung. Die Tests erfolgten bei 36 °C, einer der höchsten in Krakau gemessenen Temperaturen.
Die entscheidenden Phasen unseres Forschungsprogramms:
Anfängliche FE-Modellierung
Betriebsmodalanalyse (OMA)
Validierung der FE-Modellierung
Gebrauchstauglichkeit der Struktur unter benutzerinduzierter dynamischer Belastung
Anfängliche FE-Modellierung
Wir erstellten das Finite-Elemente-Modell der Fußgängerbrücke mit der Software ABAQUS/Standard. Eine Gesamtansicht des Modells ist in Abb. 6 dargestellt.
![Mode no.1; 2.06 [Hz] Mode no.1; 2.06 [Hz]](https://www.datocms-assets.com/53444/1739180292-mode-no-1-2-06.png) |
![Mode no.2; 3.76 [Hz] Mode no.2; 3.76 [Hz]](https://www.datocms-assets.com/53444/1739180319-mode-no-2-3-76.png) |
![Mode no.3; 5.56 [Hz] Mode no.3; 5.56 [Hz]](https://www.datocms-assets.com/53444/1739180344-mode-no-3-5-56.png) |
| Mode Nr.1; 2.06 [Hz] | Mode Nr.2; 3.76 [Hz] | Mode Nr.3; 5.56 [Hz] |
![Mode no.4; 6.52 [Hz] Mode no.4; 6.52 [Hz]](https://www.datocms-assets.com/53444/1739180369-mode-no-4-6-52.png) |
![Mode no.5; 11.85 [Hz] Mode no.5; 11.85 [Hz]](https://www.datocms-assets.com/53444/1739180399-mode-no-5-11-85.png) |
![Mode no.6; 12.23 [Hz] Mode no.6; 12.23 [Hz]](https://www.datocms-assets.com/53444/1739180414-mode-no-6-12-23.png) |
| Mode Nr.4; 6.52 [Hz] | Mode Nr.5; 11.85 [Hz] | Mode Nr.6; 12.23 [Hz] |
![Mode no.7; 15.72 [Hz] Mode no.7; 15.72 [Hz]](https://www.datocms-assets.com/53444/1739180437-mode-no-7-15-72.png) |
![Mode no.8; 19.71 [Hz] Mode no.8; 19.71 [Hz]](https://www.datocms-assets.com/53444/1739180476-mode-no-8-19-71.png) |
![Mode no.9; 20.62 [Hz] Mode no.9; 20.62 [Hz]](https://www.datocms-assets.com/53444/1739180496-mode-no-9-20-62.png) |
| Mode Nr.7; 15.72 [Hz] | Mode Nr.8; 19.71 [Hz] | Mode Nr.9; 20.62 [Hz |
Betriebsmodalanalyse (OMA)
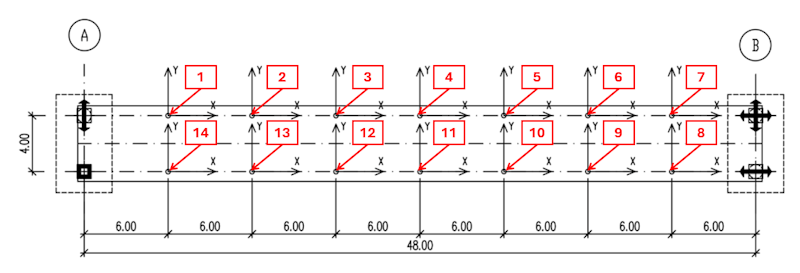
Die Modalparameter der Fußgängerbrücke wurden experimentell durch Messungen und Analyse der durch Umgebungseinflüsse hervorgerufenen Schwingungen ermittelt. Zu diesem Zweck erfassten wir Messdaten an verschiedenen Punkten (siehe Abb. 7 links).
An allen Messpunkten wurden die Signale in drei Raumrichtungen mit einer Abtastrate von 500 Hz aufgezeichnet. Für die abschließende Signalverarbeitung wurden 1800-Sekunden-Datensegmente verwendet. Abb. 8 zeigt exemplarisch den zeitlichen Verlauf von Beschleunigung und Frequenz.
Überwachungskonfiguration
Die Feldmessungen wurden durchgeführt, um die dynamischen Eigenschaften der Brücke und ihre Reaktion auf verschiedene personinduzierte dynamische Belastungen zu untersuchen. Wir platzierten die Sensoren gemäß dem FE-Modell entlang des Brückendecks, um eine fundierte Einschätzung der erwarteten dynamischen Eigenschaften des Systems zu erhalten. Um das longitudinale, laterale und vertikale Verhalten des Systems zu untersuchen, brachten wir je sieben triaxiale Beschleunigungssensoren gleichmäßig verteilt auf beiden Seiten des Brückendecks an. Insgesamt wurden 14 Messpunkte an der Struktur eingerichtet (siehe Abb. 7 links).
Überwachungsinstrumentierung
Während der Überwachungskampagne verwendeten wir den rauscharmen (25 μg√Hz spektrale Rauschdichte) triaxialen Beschleunigungssensor IOLITEiw-3xMEMS-ACC von Dewesoft mit integrierter Datenerfassung und EtherCAT-Schnittstelle. Das Gerät ist gemäß Schutzart IP67 vollständig wasserdicht ausgeführt. Es misst strukturelle Beschleunigungen in X-, Y- und Z-Richtung sowie statische Neigungen und Auslenkungen (siehe Abb. 7 rechts).
Verwendete Hard- und Software
FlexPro
Simcenter Testlab
Für die Signalverarbeitung, Datenaufzeichnung, Analyse und Visualisierung bei der Überwachung verwendeten wir die Software DewesoftX. Die aufgezeichneten Daten wurden außerdem problemlos nach FlexPro, Simcenter Testlab, Lab sowie Dewesoft Artemis OMA, das das direkte Einlesen von DewesoftX-Datendateien unterstützt, exportiert.

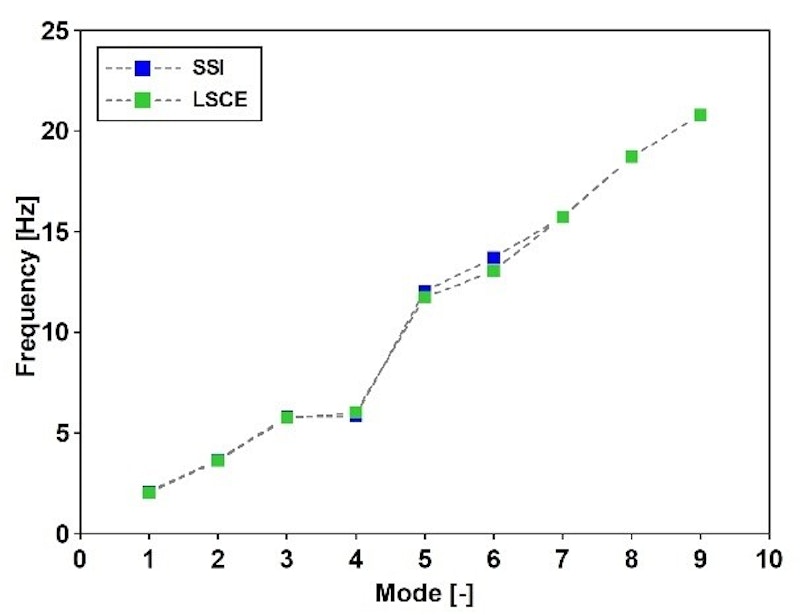
Die modalen Frequenzen und Dämpfungswerte der Fußgängerbrücke wurden mit der Least-Squares-Complex-Exponential-Methode (LSCE) und der stochastischen Unterraum-Identifikation (stochastic subspace identification, SSI) berechnet. Diese Methoden wurden zur Abschätzung der Eigenfrequenzen des experimentellen Modalmodells verwendet.
Zudem erfolgte auf Grundlage desselben Ansatzes eine Sensitivitätsanalyse der verschiedenen Modalmodelle. Die Ergebnisse der Versuchskampagne vom Sommer 2024 wurden zunächst mit den Ergebnissen des dynamischen Belastungstests vom Herbst 2021 verglichen (siehe Abb. 9).
Das experimentelle Modalmodell wurde unter Nutzung der LSCE-Methode als Referenz ermittelt. Abb. 10 zeigt die zur Erstellung und Validierung des Modalmodells herangezogenen Leitindikatoren.
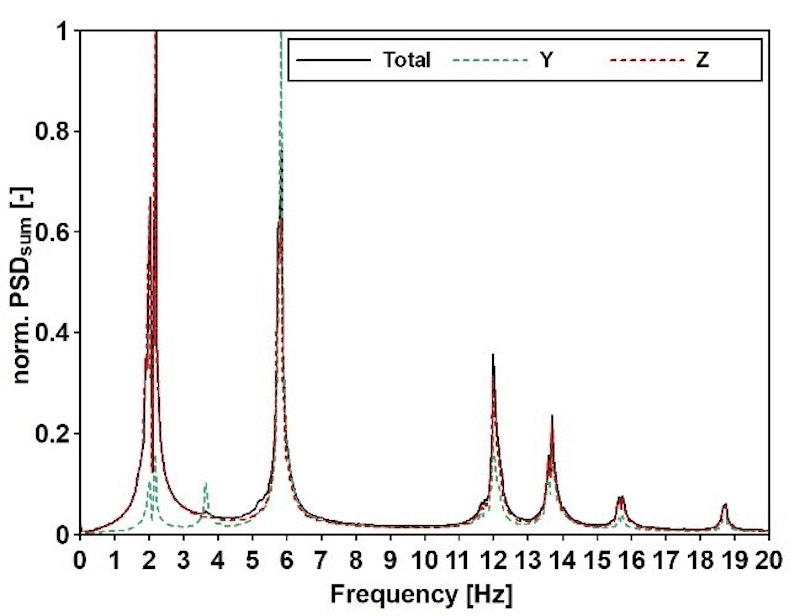
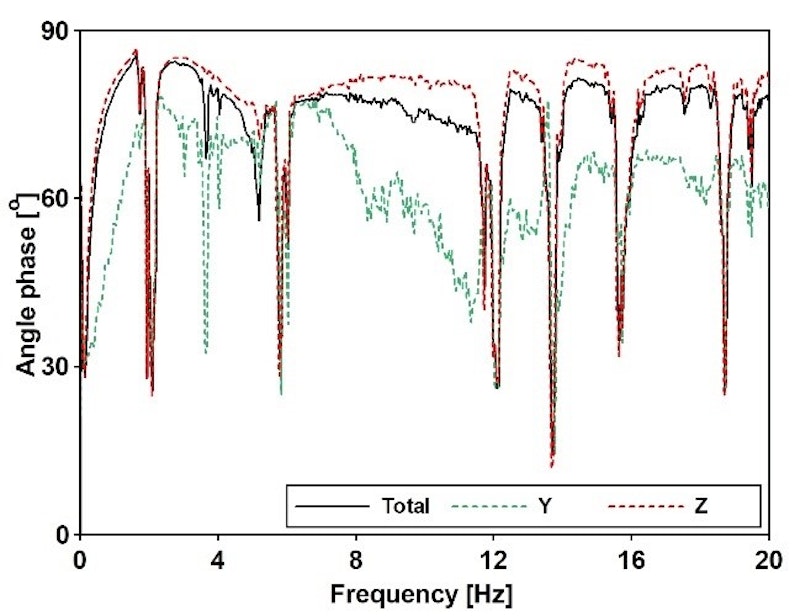
Für die Entwicklung eines zweiten experimentellen Modalmodells nutzten wir die seismische Boden-Bauwerk-Wechselwirkung (BBW), wobei wir das Bauwerk mithilfe des Antwortspektrenverfahrens untersuchten. Ein BBW-Modell berücksichtigt die Kopplung der horizontalen und kippenden Bewegungen des Fundaments.
In dieser Phase verwendeten wir Dewesoft Artemis OMA, eine Software-Suite, die für die strukturdynamische Analyse von Ingenieurbauwerken, Maschinen und anderen Strukturen ausgelegt ist, die sich nur schwer kontrolliert anregen lassen.
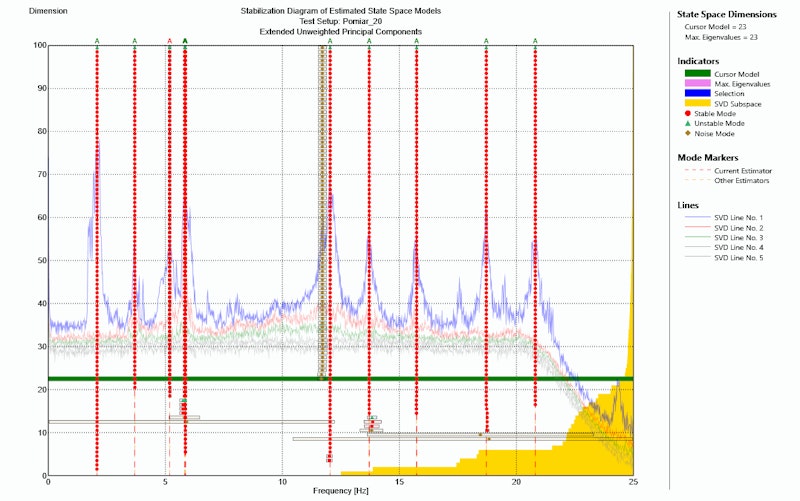
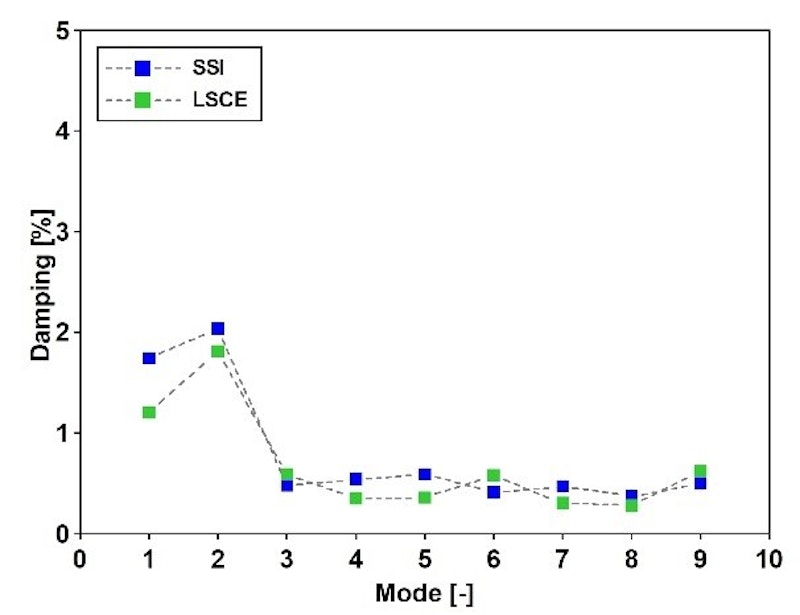
Modalparameter wie Eigenformen, Eigenfrequenzen oder Dämpfungsverhältnisse lassen sich an den Strukturen unter operationellen Bedingungen bestimmen, wobei ausschließlich die Ausgangsantwortdaten erfasst werden. Abb. 11 zeigt das zugehörige Stabilitätsdiagramm, während die folgende Tabelle und Abb. 12 die Eigenfrequenzen und Dämpfungswerte enthalten.
| Mode | LSCE | SSI | Differenz [%] | |||
|
f [Hz] |
δ [%] |
f [Hz] |
δ [%] |
f |
δ |
|
|
1V |
2.03 |
1.20 |
2.10 |
1.74 |
3.30 |
45.17 |
|
2H |
3.62 |
1.81 |
3.68 |
2.04 |
1.77 |
12.76 |
|
3V |
5.76 |
0.59 |
5.81 |
0.48 |
0.85 |
18.81 |
|
4T |
6.03 |
0.35 |
5.86 |
0.54 |
2.80 |
53.71 |
|
5V |
11.75 |
0.36 |
12.04 |
0.59 |
2.49 |
63.61 |
|
6T |
13.06 |
0.58 |
13.72 |
0.41 |
5.08 |
28.97 |
Validierung der FE-Modellierung
Auf Grundlage der experimentellen Modalmodelle bewerteten wir die Übereinstimmung zwischen der FE-Analyse und den Felddaten. Die Ergebnisse der Sensitivitätsanalyse der FE-Modellierung sind in der nachstehenden Tabelle dargestellt.
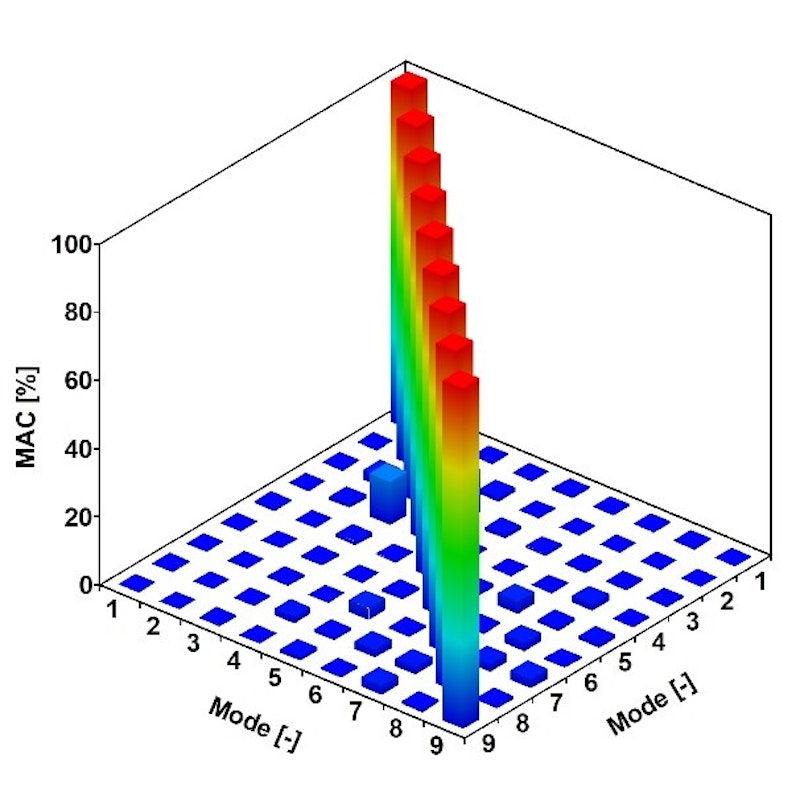
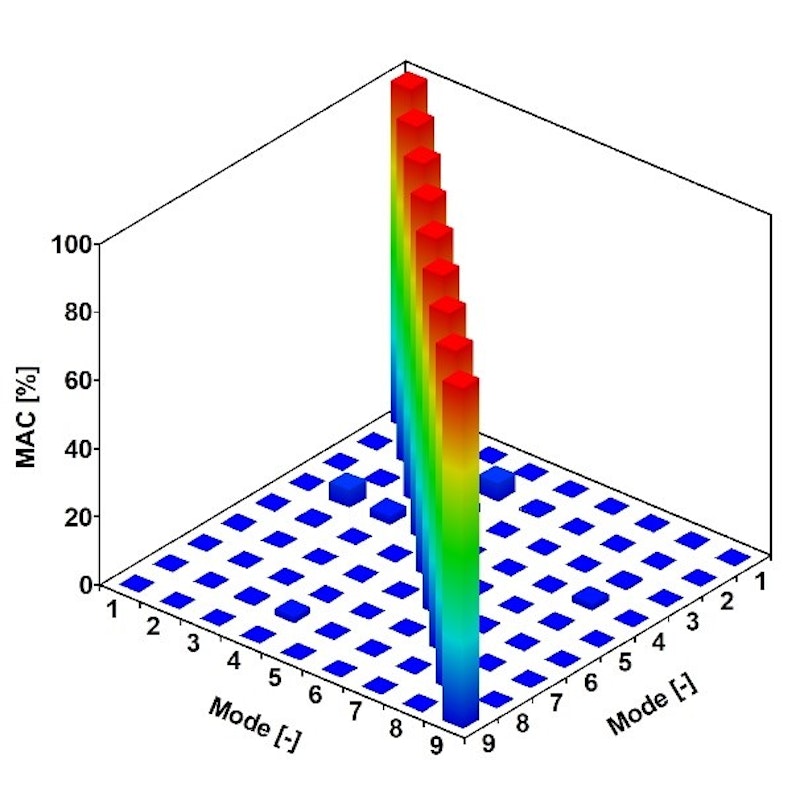
Zum Vergleich der experimentellen und numerischen Modalmodelle des Bauwerks griffen wir auf die mit der LSCE-Methode ermittelten experimentellen Ergebnisse zurück. Im Rahmen der Sensitivitätsanalyse des FE-Modells verglichen wir die Eigenfrequenzen und Eigenformen. Für den Abgleich der Moden aus der FE-Analyse (siehe Abb. 5) mit denen der OMA verwendeten wir das Modal Assurance Criterion (MAC) und die Normalized Modal Difference (NMD).
Beide Kriterien sind etablierte Instrumente zur Bewertung der Korrelation und Qualität von Eigenformen in der Strukturdynamik.
Modal Assurance Criterion (MAC): Das MAC ist ein statistischer Indikator, mit dem zwei Eigenformen durch Bewertung ihrer Ähnlichkeit verglichen werden können. Die Werte der MAC-Matrix liegen zwischen 0 und 1, wobei 1 für eine perfekte Korrelation (identische Eigenformen) steht und Werte nahe 0 eine geringe oder keine Ähnlichkeit anzeigen. Das MAC wird häufig verwendet, um die Genauigkeit experimenteller Eigenformen im Vergleich mit analytischen oder numerischen Modellen zu überprüfen.
Normalized Modal Difference (NMD): Die NMD vergleicht ebenfalls Eigenformen, quantifiziert die Differenz zwischen zwei Eigenformen aber als Prozentwert und gibt so Aufschluss über den Grad ihrer Unähnlichkeit. Im Gegensatz zum MAC zeigen niedrigere NMD-Werte dementsprechend eine größere Ähnlichkeit an, wobei 0 % bedeutet, dass die Eigenformen identisch sind.
MAC und NMD sind für die Validierung und Verfeinerung von Modalanalysen unerlässlich, da sie genaue Vergleiche zwischen gemessenen und berechneten Eigenformen gewährleisten.
| Mode [-] |
Frequenz |
Fehler [%] | |||
| LSCE | FE Model | ||||
|
1V |
2.03 |
2.06 |
1.48 |
0.96 |
0.20 |
|
2H |
3.62 |
3.76 |
3.87 |
0.93 |
0.27 |
|
3V |
5.76 |
5.56 |
3.47 |
0.95 |
0.23 |
|
4T |
6.03 |
6.52 |
8.13 |
0.92 |
0.29 |
|
5V |
11.75 |
11.85 |
0.85 |
0.96 |
0.20 |
|
6T |
13.06 |
12.23 |
6.36 |
0.89 |
0.35 |
|
7V |
15.71 |
15.72 |
0.06 |
0.95 |
0.23 |
|
8T |
18.71 |
19.71 |
5.33 |
0.88 |
0.37 |
|
9V |
20.79 |
20.62 |
0.82 |
0.94 |
0.25 |
Gebrauchstauglichkeit der Struktur unter nutzerinduzierten dynamischen Lasten
Resonanzbedingungen werden herangezogen, um das dynamische Verhalten von Fußgängerbrücken im Hinblick auf Komfortkriterien zu bewerten. Daher wurden periodische, durch Fußgänger erzeugte Belastungen analysiert, deren Frequenz mit der der kritischsten Eigenform übereinstimmt.
Unter Verwendung der experimentellen und numerischen Modalmodelle der Brücke passten wir wesentliche Parameter der Fußgängerbewegung – wie die Schrittfrequenz – für weiterführende Analysen an. Darüber hinaus bewerteten wir anhand der Feldversuchsergebnisse die dynamische Reaktion der Brücke auf Fußgängerverkehr.
Wir untersuchten experimentell drei Arten von Nutzereinwirkungen:
Nutzerinduzierter Frequenzsweep (1,5–3,5 Hz)
Passage von Fußgängern
Passage von Läufern
Abb. 13 zeigt die Ergebnisse des nutzerinduzierten Frequenzsweeps (1,5–3,5 Hz) im Zeitbereich. Die Analyse der Kurzzeit-Fourier-Transformation (short-time Fourier transform, STFT) ergab, dass sieben Eigenfrequenzen angeregt wurden. Hervorzuheben ist, dass die beiden ersten vertikalen Moden unter Resonanzbedingungen auftraten.
Die STFT-Analyse ist eine Technik zur Analyse des Frequenzgehalts nichtstationärer Signale im Zeitverlauf. Durch Unterteilung des Signals in kleine, sich überlappende Zeitabschnitte (Fenster) berechnet die STFT die Fourier-Transformation für jeden Abschnitt und ermöglicht so die Beobachtung der Veränderung der Frequenzkomponenten über die Zeit. Das Ergebnis wird häufig in einem Spektrogramm dargestellt, wobei die Farbintensität die Amplitude der Frequenzkomponenten bei jedem Zeitschritt anzeigt.
Fazit
Die einfeldrige Stahl-Beton-Verbundbrücke – Teil der Łagiewnicka-Route in Krakau – zeigt unter dynamischen Belastungsbedingungen ein stabiles und zuverlässiges Verhalten. Durch umfassende Feldversuche und Finite-Elemente-Modellierung (FE) haben wir die Eigenfrequenzen, Eigenformen und Dämpfungswerte der Brücke eingehend untersucht.
Die Übereinstimmung zwischen den experimentellen Daten und den FE-Modellvorhersagen bestätigt die Robustheit und Genauigkeit des Entwurfs. Die Brücke ist demnach in der Lage, fußgängerinduzierte Schwingungen ohne Beeinträchtigung der Sicherheit oder des Komforts zu aufzunehmen.
Brückenbauingenieurin Dr. Izabela Drygala resümiert:
Die Messkampagne war wichtig, um dynamische Daten über das Verhalten der Fußgängerbrücke unter verschiedenen Belastungs- und Umgebungsbedingungen zu erfassen. Ein solcher Ansatz ist unerlässlich für die Bewertung der Sicherheit, Leistungsfähigkeit und Dauerhaftigkeit der Brücke über ihren gesamten Lebenszyklus hinweg.
Die Ergebnisse unterstreichen die Effektivität der Stahl-Beton-Verbundbauweise der Brücke und validieren sowohl die Konfiguration des Überwachungssystems als auch die eingesetzten Analysemethoden. Die Erkenntnisse aus unserer Studie belegen die Gebrauchstauglichkeit und Widerstandsfähigkeit der Brücke im Langzeitbetrieb und liefern wertvolle Daten zur Verfeinerung dynamischer Modelle und Verbesserung der zukünftigen strukturelle Zustandsüberwachung. Diese Untersuchung setzt einen Maßstab für die Anwendung vergleichbarer Methoden zur Bewertung ähnlicher Infrastrukturbauten und trägt letztendlich zu einer höheren Sicherheit und Haltbarkeit von Fußgängerbrücken bei.