Montag, 15. Juli 2024 · 0 min read
Dynamische Charakterisierung einer zweifeldrigen Fußgängerbrücke
Bei der Königlichen Technischen Hochschule in Stockholm (Schweden) gibt es eine Fußgängerbrücke, die eine Straße und mehrere Bahngleise überspannt. Vor kurzem hat sich die Hochschule mit zwei Unternehmen – Strusoft und Dewesoft – zusammengetan, um die dynamischen Eigenschaften dieser Brücke zu untersuchen, zu analysieren und zu überwachen. Die gesammelten Daten sollen den Studierenden helfen, zu lernen, wie man die strukturdynamischen Eigenschaften von Brücken bewertet und Modelle feiner abstimmt.
Die Kungliga Tekniska Högskolan (KTH) ist die größte technische Universität in Schweden. Das Brückenmonitoring-Projekt, mit dem wir uns hier befassen, wurde von der Abteilung für Hochbau und Brücken des Fachbereichs Bauwesen und Architektur der KTH entwickelt. Das von Professor Raeid Karoumi geleitete Gemeinschaftsprojekt begann im September 2023 mit dem Aufbau einer Open-Source-Brückendatenbank als eines der zentralen Anliegen.
Künftige Doktoranden können diese Daten nutzen, um zu lernen, wie man EMA/OMA durchführt und mathematische Finite-Elemente-Modelle (FEM) mithilfe realer Daten kalibriert, und zu erfahren, wie sich unterschiedliche Bedingungen und Belastungen auf das dynamische Verhalten von Brücken auswirken und wie man den Zustand einer Brücke beurteilt und ihre Instandhaltung plant.
An dem Gemeinschaftsprojekt sind Strusoft und Dewesoft beteiligt. Strusoft ist ein schwedisches Softwareunternehmen, das Strukturdesign-Software entwickelt, die Ingenieure bei der Analyse, dem Entwurf, der Herstellung und dem Aufbau von Gebäuden und anderen Strukturen unterstützt. Dewesoft ist ein slowenischer Anbieter von Monitoring-Instrumenten, wie z. B. Sensoren, Datenerfassungsgeräten mit Software und Datenbanken.
Im Rahmen des Projekts übernahm die KTH die Installation und die Datenauswertung, während Strusoft die Software für die Erstellung der FEM von der Brücke lieferte. Von Dewesoft kamen die Beschleunigungs- und Temperatursensoren, die Datenerfassungshardware, der IEPE-Eingang für die Durchführung der Impulshammertests und die Analysesoftware, einschließlich der Module für die experimentelle Modalanalyse (EMA) und die Betriebsmodalanalyse (OMA).
Für den KTH-Beitrag war der Bauingenieur Daniel Colmenares Herrera, Ph.D., verantwortlich, bei Strusoft Shaho Ruhani, M.Sc. in Bauingenieurwesen und Stadtplanung, und bei Dewesoft Monitoring-Geschäftsentwickler Rok Mesar und der Country Manager für Schweden, Tobias Ljunggren.
Das Brückenmonitoring
Die zweifeldrige KTH-Brücke bietet einen sicheren Übergang für Fußgänger im Stockholmer Viertel Albano. Sie verbindet den KTH-Campus mit der Innenstadt und überspannt dabei eine Straße und mehrere Bahngleise.
Da sich die Brücke beim KTH-Campus und damit in einer stark belebten Gegend befindet, gelten für ihren Komfort besonders strenge Kriterien, und die Bewertung ihres dynamischen Verhaltens wird zu einer wichtigen Aufgabe.
Die Brücke weist mehrere Eigenfrequenzen unter 6 Hz auf. Solche Brücken können ein schlechtes dynamisches Verhalten zeigen, wenn sie von Menschen verursachten Belastungen ausgesetzt sind, und möglicherweise den Grenzzustand der Gebrauchstauglichkeit überschreiten.
Außerdem ist es möglich, dass sie unter sommerlichen und winterlichen Wetterbedingungen unterschiedliche dynamische Eigenschaften (Frequenzen und Dämpfung) aufweisen. Eine dynamische Bewertung unter operationellen und resonanznahen Bedingungen trägt zu einer besseren technischen Entscheidungsfindung hinsichtlich der Instandhaltung bei.
Das Monitoring ermöglicht es der KTH, die dynamischen Eigenschaften des Systems – Frequenzen, Dämpfung und Eigenformen – zuverlässig zu bestimmen. Diese wiederum erlauben die Kalibrierung eines kompletten Finite-Elemente-Modells (FE) für verschiedene Wetterbedingungen. Die Hochschule kann so die inhärenten Systemeigenschaften beobachten und über die Zeit vergleichen, um den Zustand der Brücke realistischer zu beurteilen. Kurzum: Die Ingenieure werden in die Lage versetzt, Brückenschäden zu identifizieren und frühzeitig rationale Entscheidungen zur Instandhaltung zu treffen.
Die KTH-Brücke
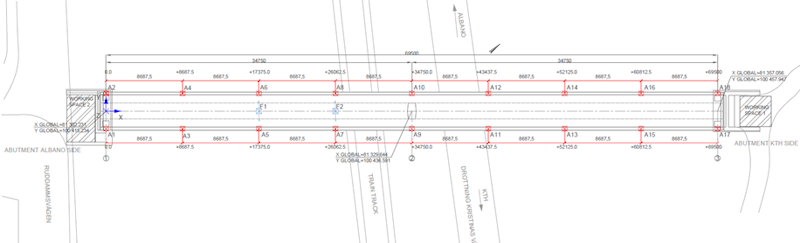
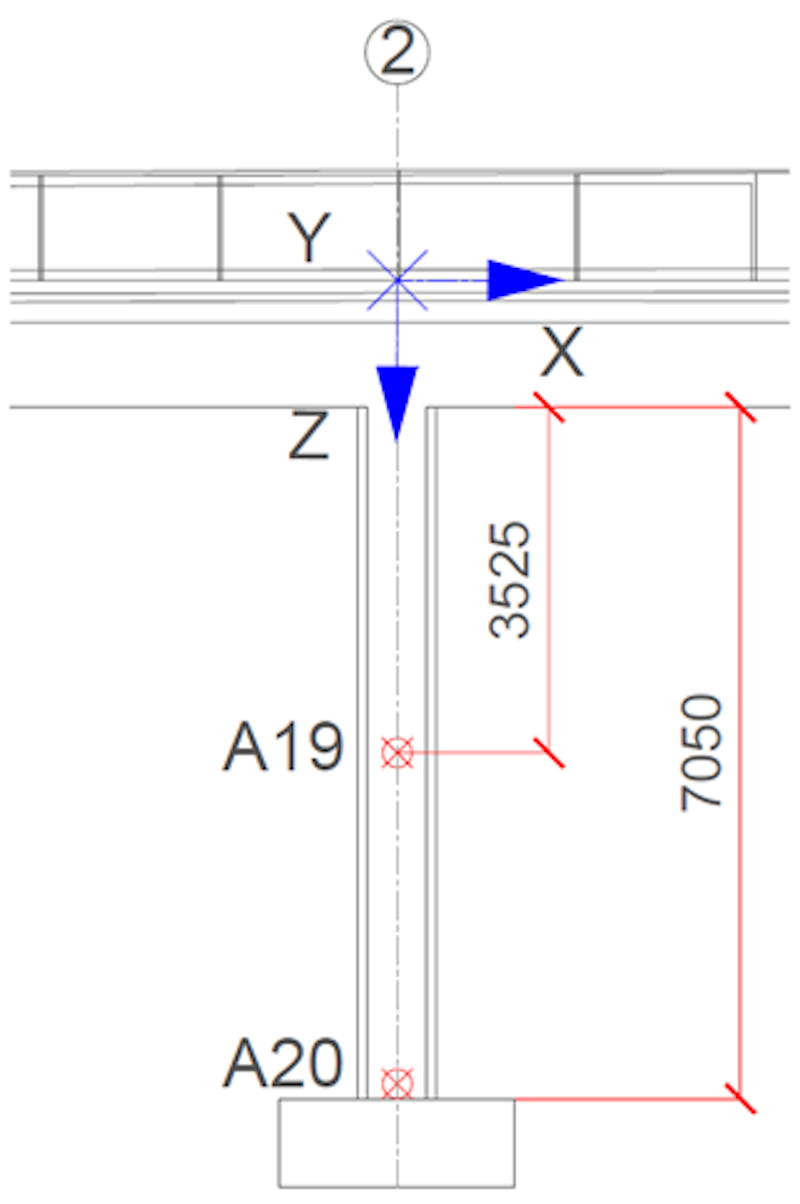
Die Fußgängerbrücke bei der KTH besteht im Wesentlichen aus einem durchgehenden zweifeldrigen nachgespannten Betonträger (siehe Abb. 2). Die Spannweite der Brückenfelder beträgt jeweils 34,75 m, mit einem mittig angeordneten, 9 m hohen Stützpfeiler. Das Brückendeck liegt an den Enden beider Spannweiten auf Widerlagern auf.
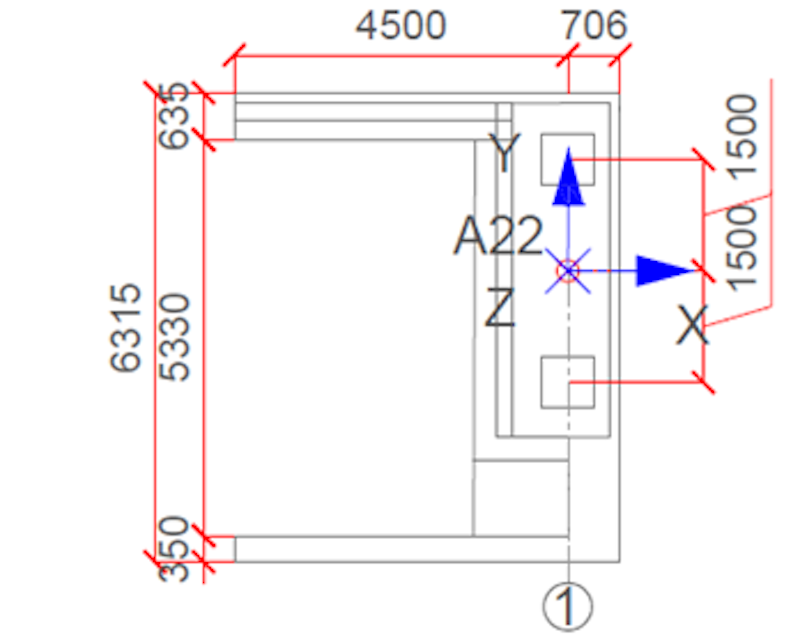
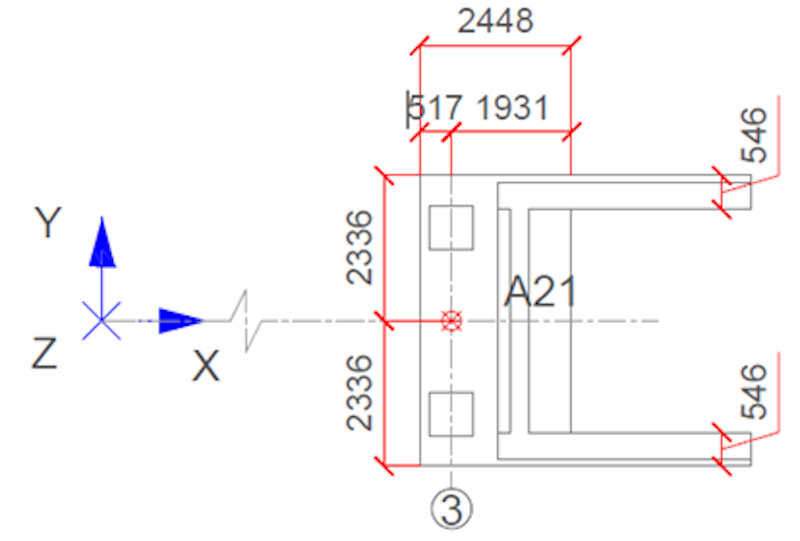
Der Querschnitt des Brückendecks variiert (siehe Abb. 3). Abb. 4 zeigt die entsprechende Variation der Querschnittsträgheit und -fläche. Nach schwedischem Standard sind das Brückendeck aus Beton der Klasse K45 und die Stützpfeiler aus aus Beton der Klasse K40 gefertigt. Der Einfluss der nachgespannten Kabel wurde nicht untersucht.
Grobe Eigenwertanalyse
Wir schätzten die dynamischen Eigenschaften der Brücke anhand von Handbuchformeln. Für die beschriebene Längsmode der Brücke pauschalierten wir die Masse am oberen Ende des Stützpfeilers. Die modale Masse des Pfeilers bezogen wir in das äquivalente SDOF-System ein (24,24 % der Masse des Pfeilers). Siehe die Ergebnisse in Tabelle 1
Für die erste Biegemode nahmen wir an, dass sich der Stützpfeiler wie ein Gelenklager verhält, das einem zweifeldrigen Trägersystem entspricht. So konnten wir die erste Biegemode als volle Sinusfunktion abschätzen (zweite Biegemode eines einfach gestützten Trägersystems). Siehe die Ergebnisse in Tabelle 1
| L_b [m] | 69.5 |
| E_b [Pa] | 3.40E+10 |
| (assumed) I_b [m^4] | 0.3 |
| L_c (free length) [m] | 7 |
| m_b [kg] | 440160 |
| m_c [kg] | 31104 |
| 24,24 % m_c [kg] | 7539.6096 |
| E_c [Pa] | 3.30E+10 |
| I_c [m^4] | 0.0768 |
| k_c | 3 E_c I_c / L_c^3 |
| f1_long [Hz] | 1.12 |
| f1_bending [Hz] | 1.65 |
Ergebnisse früherer Messkampagnen
Tabelle 2 zeigt die Ergebnisse der bei herbstlichen Wetterbedingungen (15,4 °C) durchgeführten Messkampagne, die wir mit denen der neuen Messkampagne vergleichen werden, die bei winterlichem Wetter (-5 °C) durchgeführt wurde.
| Mode | Natural frequency [Hz] | Damping [%] |
|---|---|---|
| 1 (Bending) | 1.77 | 1.4 |
| 2 (Bending) | 2.68 | 1.1 |
| 3 (Lateral) | 2.81 | 0.6 |
| 4 (Bending) | 5.61 | 1.1 |
| 5 (Lateral) | 5.37 | 0.7 |
| 6 (Bending) | 7.27 | 2.5 |
Monitoring-Setup
Die Feldmessungen wurden durchgeführt, um die dynamischen Eigenschaften und das dynamische Verhalten unter verschiedenen Belastungsszenarien zu messen und zu untersuchen. Wir platzierten die Sensoren nach Vorgabe eines FE-Modells entlang des Brückendecks, um eine fundierte Vorstellung von den erwarteten dynamischen Eigenschaften des Systems zu erhalten.
Um das longitudinale, laterale und vertikale Verhalten des Systems zu untersuchen, verteilten wir 18 triaxiale Beschleunigungssensoren gleichmäßig auf beiden Seiten des Brückendecks. Zwei zusätzliche triaxiale Beschleunigungssensoren am vertikalen Stützpfeiler der Brücke dienten der Erfassung und Bewertung des dynamischen Verhaltens des Pfeilers und seines Beitrags zum Gesamtsystem.
An jedem Widerlager wurde je ein weiterer triaxialer Beschleunigungssensor angebracht, um die potenziell von vorbeifahrenden Zügen verursachten Schwingungen zu bewerten und das Modell für die mögliche Boden-Bauwerk-Interaktion (Soil-structure interaction, SSI) zu kalibrieren. Abb. 5 zeigt eine schematische Darstellung des Messplans, Abb. 6 die Anordnung der Messinstrumente an der Brücke. Die Anzahl der Beschleunigungssensoren und ihre Verteilung helfen, räumliches Aliasing bei Schwingungsmoden höherer Ordnung zu vermeiden.
In unserer ersten Versuchskampagne führten wir einen Impulshammertest an den Punkten F1 und F2 durch. Auf das Anregungs- und Antwortsignal wendeten wir ein Kraft- und ein Exponentialfenster an, um die Kohärenzfunktion des Frequenzgangsschätzers (FRF-Schätzer) zu verbessern.
Wir schätzten die FRFs, indem wir das Autoleistungsdichtespektrum des Eingangssignals und das Kreuzleistungsdichtespektrum zwischen Eingangs- und Ausgangssignal berechneten und dabei den H1-Schätzer verwendeten. Zur Verbesserung der Qualität der FRFs mittelten wir die Ergebnisse mehrerer Impulshammerschläge.
Auf die gemessenen Daten wurde eine digitale Signalverarbeitung angewendet. Zur Verarbeitung der Signale (0,1 bis 25 Hz) für den Impulshammertest wurde ein Nullphasen-Bandpassfilter eingesetzt. Die Kraft- und Exponentialfenster verbesserten die Kohärenzfunktion, indem sie die Kausalität der aufgezeichneten Signale konsistent verbesserten.
Auf diese Weise gelang es uns, das Doppel-Klingeln zu minimieren und den inhärenten Rauschanteil in den Daten zu reduzieren. Ein Korrekturfaktor wurde angewendet, um den passenden Schätzer für das Dämpfungsverhältnis zu erhalten, da das Exponentialfenster eine künstliche Dämpfung hinzufügt.
Überwachungsinstrumentierung
IOLITEiw-3xMEMS-ACC – ein triaxialer, rauscharmer (spektrale Rauschdichte 25 μg√Hz) Beschleunigungssensor mit integrierter Datenerfassung und EtherCAT-Schnittstelle. Das Gerät ist vollständig wasserdicht (Schutzart IP67) und kann strukturelle Beschleunigungen in der X-, Y- und Z-Achse sowie statische Neigungen und Auslenkungen messen.
IOLITEiw-3xMEMS-ACC-T – ein triaxialer, rauscharmer (spektrale Rauschdichte 25 μg√Hz) Beschleunigungssensor mit externem digitalen Temperatursensor, integrierter Datenerfassung und EtherCAT-Schnittstelle. Das Gerät ist vollständig wasserdicht (Schutzart IP67) und kann strukturelle Beschleunigungen in der X-, Y- und Z-Achse sowie statische Neigungen und Auslenkungen messen.
IOLITE-1xACC – ein hochwertiger Signalaufbereiter für IEPE-Sensoren. In diesem Fall verwendeten wir ihn zum Auslesen der Daten vom Dytran-Impulshammer.
Dytran 5803A – ein IEPE-Impulshammer mit definierbarer Impulskraft zur Anregung größerer Strukturen im Rahmen der Untersuchung ihres dynamischen Verhaltens
Installation
Am 28. November 2023 installierten wir das System unter schwierigen Wetterbedingungen mit Temperaturen von bis zu -5 °C und Schnee.
Für die Positionierung der Beschleunigungssensoren am Brückendeck verwendeten wir speziell entwickelte robuste Halterungen. Zur Beschleunigung des Prozesses hatten wir im Vorfeld zwei spezielle Halterungstypen entwickelt, die es uns ermöglichten, die Geräte mühelos ohne Verschraubung oder Verklebung anzubringen.
An den Pfeilern konnten die Module sicher mit einem speziellen silikonbasierten Klebstoff befestigt werden.
Monitoring-Software
Die verwendete Lösung kombinierte mehrere Softwareprodukte:
Datenerfassungssoftware DewesoftX – Test- und Messdatenerfassungssoftware für die Datenaufzeichnung, Signalverarbeitung und Datenvisualisierung
Dewesoft Historian – Softwaredienst für langfristige und permanente Überwachungsaufgaben mit Messdatenspeicherung in einer InfluxDB-Zeitreihendatenbank
Dewesoft Artemis OMA – Software-Suite zur Analyse der Strukturdynamik von Bauwerken, Maschinen und anderen nur schwer in kontrollierbarer Weise anregbaren Strukturen aller Art. Modalparameter wie Eigenformen, Eigenfrequenzen oder Dämpfungsverhältnisse lassen sich an den Strukturen unter operationellen Bedingungen bestimmen, indem nur die Ausgangsantwortdaten erfasst werden.
Dewesoft-Modaltest und -Modalanalyse – Softwarepaket für die strukturdynamische Analyse von Ingenieurbauwerken, Maschinen und anderen per Impulshammer oder Shaker künstlich und kontrolliert angeregten Strukturen aller Art. Modalparameter wie Eigenformen, Eigenfrequenzen oder Dämpfungsverhältnisse lassen sich an den Strukturen unter operationellen Bedingungen bestimmen, indem Eingangs-/Anregungsdaten und Ausgangs-/Antwortdaten erfasst werden. Die Software ist für die Durchführung von OMA (Betriebsmodalanalysen), EMA (experimentellen Modalanalysen) und ODS (Betriebsschwingformanalysen) geeignet.
Strusoft FEM-Design – Fortschrittliche, intuitive Strukturanalysesoftware, die alle bautechnischen Anforderungen unterstützt. Die Software erlaubt die 3D-Modellierung, Planung und Finite-Elemente-Analyse (FEA) von Beton-, Stahl-, Holz-, Verbund-, Mauerwerks- und Fundamentstrukturen. Alle Berechnungen entsprechen den Eurocode-Normen, einschließlich einiger spezifischer nationaler Anhänge.
Messanordnung – OMA (Betriebsmodalanalyse)
Für die Beschleunigungsanalyse verwendeten wir ein System mit der Software Dewesoft ARTeMIS OMA, einem IP65-Schrank mit Industrie-PC, der Software DewesoftX, USV, PWIN und einer Stromversorgung sowie kapazitive triaxiale MEMS-Sensoren mit geringer Rauschdichte.
Die Beschleunigungssensoren sind in den IOLITEiw-3xMEMS-ACC mit EtherCAT-Schnittstelle integriert. Wo Temperatur und Beschleunigung gemessen werden mussten, installierten wir Module des Typs IOLITEiw-3xMEMS-ACC-T, die neben dem Beschleunigungssensor auch einen Temperatursensor umfassen. Ein im IOLITE 3xMEMS verbauter Mikroprozessor überträgt die Messwerte an die auf einem Windows-PC laufende DewesoftX-Software oder einen beliebigen EtherCAT-Master-Controller.
Wir erfassten die Daten mit einer Abtastrate von 200 S/s und speicherten sie in einer vierstündigen DXD-Datei, die wir später zur Analyse in Dewesoft ARTeMIS OMA importierten.
OMA-Schritte
Für die Datenerfassung, Geometrie und Zuordnung der Freiheitsgrade (DOF) verwendeten wir die Software DewesoftX. DewesoftX generierte eine UNF-Datei für den Geometrieexport und eine DXD-Datei für die Daten, die wir in Dewesoft ARTeMIS OMA importierten.
Für die Analyse/Vorbereitung der Daten wählten wir eine Reduktion auf 20 Hz und verwendeten die Methode der erweiterten Frequenzbereichszerlegung (Enhanced Frequency Domain Decomposition, EFDD).
Ergebnisse der OMA
Wir führten eine Betriebsmodalanalyse durch, um die Eigenfrequenzen der Brücke, die Dämpfungsverhältnisse und die Eigenformen zu ermitteln.
| Modus | Frequenz (Hz) | Dämpfung (%) |
|---|---|---|
| 1. (bending) | 2.22 | 2.1 |
| 2. (bending) | 3.03 | 2.2 |
| 3. (lateral) | 6.09 | 0.9 |
| 4. (bending) | 6.97 | 0.8 |
| 5. (bending) | 8.32 | 0.8 |
| 6. (lateral) | 11.39 | 2.1 |
Messanordnung – EMA (experimentelle Modalanalyse)
Für die künstliche Anregung der Struktur an den Punkten F1 und F2 (siehe Abb. 6) verwendeten wir einen IEPE-Impulshammer des Typs Dytran 5803A.
Die Messanordnung umfasste die Software Dewesoft Modal Testing and Modal Analysis, einen IP65-Schrank mit Industrie-PC, die Software DewesoftX, USV, PWIN und eine Stromversorgung sowie kapazitive triaxiale MEMS-Sensoren mit geringer Rauschdichte und einen Impuls- bzw. Modalhammer
EMA-Schritte
Im Modul Dewesoft Modal Testing wählten wir die Impulshammer-Anregung und die Option Roving Hammer (wandernder Hammer), die es uns erlaubte, die Struktur an mehreren Punkten anzuregen. Außerdem mussten wir eine passende Frequenzauflösung festlegen, um die Größe des Zeitbereichsdatenblocks für die Berechnung eines einzelnen Blocks zu bestimmen. Die Hauptergebnisse des MT-Moduls sind die Frequenzgangfunktion (FRF) und die Kohärenzfunktion.
Gemäß dem Messplan für die Brücke sollte die Struktur an zwei Punkten angeregt werden, daher wurden zwei Anregungskanäle (Nr. 23 und Nr. 24) für den Impulshammertest erstellt. Die Auslöseschwelle wurde auf 50 N festgelegt, d. h. die Software würde keine Schläge unter dieser Schwelle erkennen. Außerdem mussten wir die Richtung und Ausrichtung der Anregungskanäle festlegen.
Wir maßen die Antworten an 22 Punkten mit triaxialen Beschleunigungssensoren und erstellten 66 Antwortkanäle (22 Punkte in jeweils drei Richtungen). Die Knoten-IDs, Richtungen und Ausrichtung mussten für jeden Punkt entsprechend definiert werden.
Wir erstellten die Geometrie der KTH-Brücke im Geometrie-Editor. Sie können Geometrien erstellen, indem Sie Objekte definieren und kombinieren, UNV-Dateien importieren oder jeden Koordinatenpunkt einzeln positionieren.
Die Strukturgeometrie konnten wir auf Grundlage der erfassten FRFs per Frequenzauswahl animieren.
Wir verwendeten das Modalanalysemodul, um Modalparameter aus den Messdaten zu extrahieren. Für die Berechnung konnten wir alle FRFs verwenden, und bei der Konfiguration der Modalanalyse definierten wir die Bandbreite und die maximale Ordnung für die Polynomial-Anpassungen.
Wir konnten die Eigenformen berechnen, indem wir die stabilen Pole manuell im Stabilisierungsdiagramm auswählten.
Ergebnisse der EMA
| Mode (ID) | Dampened frequencies (Hz) | Damping Ratios (%) |
|---|---|---|
| 1 | 2.25 | 0.861 |
| 2 | 3.10 | 0.956 |
| 3 | 6.96 | 0.923 |
| 4 | 8.30 | 1.315 |
| 5 | 13.91 | 1.225 |
| 6 | 15.83 | 1.393 |
Bei der Durchführung des Impulshammertests in vertikaler Richtung wurden keine seitlichen, hingegen aber vertikale und torsionale Schwingungsmoden angeregt.
Finite-Elemente-Modellierung
Das FE-Modell vermittelte uns eine Vorstellung von der dem System inhärenten Unbestimmtheit. Wir analysierten den Einfluss von Temperaturänderungen und deren Auswirkungen auf die dynamischen Eigenschaften des Systems.
Untersucht wurden in Einzelnen die folgenden vier Aspekte:
Änderungen des Elastizitätsmoduls des Betons
Einfluss der elastischen Randbedingungen
Einfluss der mechanischen Eigenschaften der Asphaltschicht
Einfluss der Dehnungsfuge auf die Systemeigenschaften
Dafür erstellten wir zwei Modelle, nämlich
ein Schalenmodell (Ingenieurmodell) und
ein Volumenmodell (Forschungsmodell).
Für unser Ingenieurmodell modellierten wir das Brückendeck und den Pfeiler mit neunknotigen 3D-Schalenelementen (Mindlin-Reissner-Elemente) mit einer durchschnittlichen Gitterweite von 0,1 m. Die Randträger modellierten wir mit zweiknotigen 3D-Balkenelementen (Timoshenko-Elemente) mit einer Teilungszahl von 20. Der Einfluss des vorgespannten Betons wurde im FE-Modell nicht berücksichtigt.
Wir führten eine Konvergenzanalyse der Eigenfrequenzen des Systems durch, um die Konvergenz des gewählten Gitters – ohne Berücksichtigung der Geländer – zu untersuchen (siehe Schalenmodell in Abb. 20).
Das Ingenieurmodell verwendeten wir, um den Einfluss der Unbestimmtheit der Materialeigenschaften des Betons auf die dynamischen Eigenschaften des Systems nachzuvollziehen. Dabei konzentrierten wir uns auf die Kombination mit den Auswirkungen der Randbedingungen auf die Struktur, da die Rollenlager aufgrund der Reibung an den Auflagern unter realen Betriebsbedingungen möglicherweise nicht funktionieren wie erwartet.
Die Ergebnisse der parametrischen Analyse der Eigenfrequenzen des Systems in Abhängigkeit vom Elastizitätsmodul des Betonmaterials und den Randbedingungen (Rollenlager-Rollenlager und Gelenklager-Gelenklager) sind in Abb. 21 dargestellt.
Für das Forschungsmodell verwendeten wir ein zehnknotiges quadratisches Tetraederelement mit einer anfänglichen Gitterweite von 0,6 m, für die Stahlgeländer, die sich auf der KTH-Seite vier Meter über das Brückendeck hinaus auf das Widerlager erstrecken, 3D-Euler-Bernoulli-Balkenelemente mit einer anfänglichen Gitterweite von 0,2 m. Die Asphaltschicht weist auf dem Brückendeck eine konstante Dicke von 75 mm auf und reicht nicht über das Brückendeck hinaus. Eine Darstellung des Modells ist in Abb. 22 zu sehen.
Wir bewerteten die folgenden drei Aspekte des Modells:
Einfluss der Randbedingungen
Einfluss der Materialeigenschaften des Asphalts
Einfluss der Dehnungsfuge
Den Einfluss der Randbedingungen berücksichtigten wir, indem wir eine lineare Feder in Längsrichtung der Brücke annahmen, um der Reibung an den Auflagern unter operationellen Bedingungen Rechnung zu tragen. Die Ergebnisse sind in Abb. 23 dargestellt.
Die Eigenfrequenzen der Brücke ändern sich, wenn die Federsteifigkeit K_b variiert wird, und veranschaulichen so die Abhängigkeit der dynamischen Eigenschaften des Systems von den gewählten Parametern. In Abb. 24 sehen Sie die Eigenformen des Systems in der vollen 3D-Ansicht.
Der Einfluss der Asphaltschicht auf der Brücke wurde mittels der Variation ihrer mechanischen Eigenschaften in Abhängigkeit von der Temperatur erfasst. Für die geschätzten Materialeigenschaften der Asphaltschicht unter warmen und kalten Bedingungen siehe Tabelle 5.
| T (°C) | v (-) | P (kg/m^3) | E (Gpa) |
|---|---|---|---|
| 40 | 0.40 | 2450 | 1 |
| 0 | 0.20 | 2450 | 17 |
Wir berechneten die dynamischen Eigenschaften des Systems also mittels der Variation der Eigenschaften der Asphaltschicht im FE-Modell. Abb. 25 zeigt die Ergebnisse der parametrischen Analyse der Eigenfrequenzen des Systems in Abhängigkeit vom Elastizitätsmodul der Asphaltschicht.
Es zeigte sich, dass der Einfluss der Asphaltschicht weniger ausgeprägt war als die Lagersteifigkeit der Auflager des Systems. Wir quantifizierten den Einfluss der Dehnungsfugen auf die dynamischen Eigenschaften des Systems, indem wir eine lineare Feder zwischen den Brückenenden mit den entsprechenden Widerlagern annahmen, die der Geometrie der Dehnungsfuge über eine Länge von 4,35 m (Breite der Brücke) folgte.
Die Ergebnisse der parametrischen Analyse der Eigenfrequenzen des Systems in Abhängigkeit von der elastischen Federsteifigkeit der Dehnungsfuge sind in Abb. 26 dargestellt. Die Dehnungsfugen beeinflussen vor allem die erste und fünfte Schwingungsmode des Systems.
Vergleich der Ergebnisse
In Abb. 27 sind die Veränderungen der Eigenfrequenzen des Systems infolge der Wetterbedingungen im Herbst und im Winter dargestellt.
Wir beobachteten, wie der jahreszeitliche Temperatureinfluss die Linie der Eigenfrequenzen des Systems nach oben verschiebt, also zu einer höheren Steifigkeit der Struktur führt. Außerdem wirkt sich der Einfluss der zuvor genannten Aspekte auf die Eigenfrequenzen der Brücke aus. Siehe dazu in Abb. 28 die Einflussbereiche der Asphalteigenschaften, der Dehnungsfuge und der Federsteifigkeit der Auflager im Vergleich zu den Änderungen aufgrund des Temperatureffekts.
Schließlich quantifizierten wir die Veränderung des Dämpfungsverhältnisses des Systems bei herbstlichen und winterlichen Wetterbedingungen (für die Ergebnisse siehe Abb. 29).
Fazit
Wir stellten fest, dass die Durchführung von Messungen erforderlich ist, da anders kein klarer temperaturabhängiger Trend des Modalverhältnisses definiert werden kann.
Wir können den Umfang der temperaturbedingten Änderungen der Eigenfrequenzen des Systems erklären. Er entspricht der gewichteten Summe der Änderungen der Eigenschaften der Asphaltschicht, der Dehnfugensteifigkeit und der Federsteifigkeit an den Auflagern. So waren wir in der Lage, eine komplette Systemempfindlichkeitsanalyse vorzulegen. Für zukünftige Studien könnten wir eine vollständige Kalibrierung des FE-Modells durchführen, um die Unsicherheiten des Systems nach einem physikalisch basierten Ansatz genau zu quantifizieren.
Die Ergebnisse zeigen, dass die Wetterbedingungen das dynamische Verhalten des Systems erheblich beeinflussen können. Unser Fall verdeutlicht den Bedarf an zuverlässigeren, durch Messkampagnen an Infrastrukturen unterstützten Modellen. Die Überwachung struktureller Systeme kann dazu beitragen, Schäden frühzeitig zu erkennen. Sie kann auch zu einem umfassenderen Verständnis der tatsächlichen Eigenschaften des gebauten Systems beitragen und helfen, FE-Modelle zu kalibrieren, um die Gestaltung von Brückenmanagementsystemen zu verbessern.
Wir stellten einen Vergleich zwischen dem Ingenieurmodus und dem vollen 3D-Modell an und zeigten das Problem der Eindeutigkeit der Lösung zur Kalibrierung der Modelle und ihre entsprechenden Einschränkungen auf. Es könnten weitere Messungen erforderlich sein, um die FE-Modelle zu verbessern und weiter zu kalibrieren. Zum Beispiel würde die Überwachung der Auslenkungen der Auflager die Modelle um wertvolle Systeminformationen ergänzen.
Die wertvollsten Ergebnisse dieser Arbeit sind:
der Nachweis des signifikanten Einflusses, den die Wetterbedingungen auf das dynamische Verhalten des Systems haben können,
der Nachweis der Unsicherheiten, die sich bei der FE-Modellierung sowohl bei Ingenieur- als auch bei Forschungsmodellen ergeben können, und
die Erkenntnis, dass das Monitoring für die Bewertung der Systemperformance und die Verbesserung der aktuellen technischen Praxis in Bezug auf Brückenmanagementsysteme von entscheidender Bedeutung ist.