Inhaltsübersicht
Kategorien durchsuchen
Autoren durchsuchen
 AB
ABAlberto Boffi
 AL
ALAlessia Longo
 AH
AHAl Hoge
 AB
ABAljaž Blažun
 BJ
BJBernard Jerman
 BČ
BČBojan Čontala
 CF
CFCarsten Frederiksen
 CS
CSCarsten Stjernfelt
 DC
DCDaniel Colmenares
 DF
DFDino Florjančič
 EB
EBEmanuele Burgognoni
 EK
EKEva Kalšek
 FB
FBFranck Beranger
 GR
GRGabriele Ribichini
Glacier Chen
 GS
GSGrant Maloy Smith
 HB
HBHelmut Behmüller
 IB
IBIza Burnik
 JO
JOJaka Ogorevc
 JR
JRJake Rosenthal
 JS
JSJernej Sirk
 JM
JMJohn Miller
 KM
KMKarla Yera Morales
 KD
KDKayla Day
 KS
KSKonrad Schweiger
Leslie Wang
 LS
LSLoïc Siret
 LJ
LJLuka Jerman
 MB
MBMarco Behmer
 MR
MRMarco Ribichini
 ML
MLMatic Lebar
 MS
MSMatjaž Strniša
 ME
MEMatthew Engquist
 ME
MEMichael Elmerick
 NP
NPNicolas Phan
 OM
OMOwen Maginity
 PF
PFPatrick Fu
 PR
PRPrimož Rome
 RM
RMRok Mesar
 RS
RSRupert Schwarz
 SA
SASamuele Ardizio
 SK
SKSimon Kodrič
 SG
SGSøren Linnet Gjelstrup
 TH
THThorsten Hartleb
 TV
TVTirin Varghese
 UK
UKUrban Kuhar
Valentino Pagliara
 VS
VSVid Selič
 WK
WKWill Kooiker
Schwingungsmessung und -analyse an Elektromotoren
Giacomo Boschin (Department of Engineering)
University of Trieste
March 12, 2024
Elektromotoren kommen in vielen technischen Bereichen, von industriellen Anlagen und Maschinen bis hin zu Automobilanwendungen, zum Einsatz, und wie bei anderen rotierenden Maschinen stellen Vibrationen und Lärm auch bei ihnen typische Problemfelder dar.
Das Aufkommen und die Verbreitung elektrischer Antriebe bringen Geräuschprobleme ans Licht, die Ingenieure bei Verbrennungsmotoren oft übersehen haben, da diese „neuen“ Geräusche vom Motorenlärm übertönt werden. Damit Elektromotoren einen optimalen Wirkungsgrad erreichen können, müssen Schwingungen untersucht und Frequenzen bestimmt werden.

In der modernen Technik werden rotierende Maschinen üblicherweise zur Erzeugung von Bewegung eingesetzt. Es liegt in der Natur der Sache, dass der kontinuierliche Betrieb dieser Maschinen Schwingungen erzeugt. Solche Phänomene beeinträchtigen die Maschinenleistung und können sogar zu Ausfällen führen.
Das Wissen darum, wie die Schwingungen entstehen und wie sie sich reduzieren lassen, kann über den Erfolg oder das Misslingen einer Produkteinführung entscheiden.
An der Universität Triest untersuchten und analysierten mein Team und ich mithilfe des Dewesoft-Datenerfassungssystems Schwingungsfaktoren in Elektromotoren, um unser Verständnis der Dynamik in einem Motor-Platte-System zu verbessern.
Selbst unter günstigen Bedingungen erzeugt jede Maschine Schwingungen. Viele dieser Schwingungen stehen in direktem Zusammenhang mit periodischen Ereignissen, die während des Betriebs der Maschine auftreten, wie z. B.
das Drehen einer Motorwelle,
das Ineinandergreifen von Getriebezähnen,
rotierende elektrische Felder usw.
Die Frequenz, bei der diese Ereignisse auftreten, kann auf die Schwingungsquelle hinweisen. Deshalb ist die Frequenzanalyse grundlegender Bestandteil vieler leistungsfähiger Diagnoseverfahren.
Unsere Studie hatte im Wesentlichen zwei Ziele:
die Untersuchung eines auf eine Kunststoffplatte montierten und über Federn mit dem Boden verbundenen Elektromotors durch Beobachtung seines Schwingungsverhaltens bei steigender Drehzahl und Überschreiten der Resonanzfrequenzen;
die Bestimmung der für das System kritischsten Frequenzen mit Ermittlung der möglichen Quellen der Schwingungsverstärkung
Ordnungsanalyse
Die Ordnungsanalyse ist ein perfektes Werkzeug zur Bestimmung des Betriebszustands von rotierenden Maschinen oder Kolbenmaschinen, insbesondere wenn diese mit variierenden Geschwindigkeiten laufen.
Bei der Analyse rotierender Maschinen sind zwei Eigenschaften bzw. messbare Größen von besonderem Interesse:
die Amplitude bzw. Intensität, die beschreibt, wie weit sich das Objekt bewegt, und
die Frequenz, die beschreibt, wie schnell sich das Objekt bewegt.
Zur Beschreibung der Bewegung werden die Begriffe Frequenz, Amplitude und Beschleunigung verwendet. Wie bei der Schwingungsanalyse üblich, werden auch die Strukturresonanzen (Moden) berücksichtigt, da sie die Schwingungen verstärken.
Bei rotierenden Maschinen sind zudem die direkt oder indirekt durch die Rotation selbst verursachten Vibrationen von Interesse. Sie können auch ohne Resonanzverstärkung groß werden und ihre Ursache in mechanischen Unwuchten, Achsverformungen oder -versätzen, Defekten an Lagerringen oder beschädigten Getriebezähnen haben.
Jede dieser Schwingungsquellen erzeugt Schwingungen mit einem bestimmten Vielfachen der Maschinendrehzahl. Rotierende Maschinen können drehzahlabhängige Vibrationen bei Struktureigenresonanzen und Eigenfrequenzen generieren, die oft hohe Schwingungspegel und Schwingungsprobleme verursachen und sogar katastrophale Ausfälle zur Folge haben können.
Frequenzen, die einem Vielfachen der Drehzahl entsprechen, werden als Ordnungen bezeichnet. Dabei ist die Rotationsgeschwindigkeit selbst die Ordnung 1, das Zweifache dieser Geschwindigkeit die Ordnung 2 usw. Ordnungen müssen nicht ganzzahlig sein. Man kann also z. B. auch eine Ordnung 2,5 oder 3,938 haben
Ingenieure verwenden häufig zweidimensionale Diagramme, so genannte Ordnungslinien, um zu ermitteln, wie verschiedene drehzahlabhängige Komponenten zu Schwingungs- oder Schallpegeln beitragen. Sie berechnen diese Diagramm aus der Drehzahlkarte (RPM map) und extrahieren Informationen über den quadratischen Mittelwert einer Ordnungskomponente im Verhältnis zur Drehzahl.
Schwingungsmessanordnung
Die Montage der Ausrüstung
Um Daten erfassen zu können, musste ich zunächst das physische System aufbauen. Das erste Element war ein dreiphasiger Elektromotor mit einer Nenndrehzahl von 1410 U/min. Er wurde mit 220 V (50 Hz) versorgt und in Dreieckschaltung angeschlossen.
Den Motor befestigte ich mit Schrauben und Muttern auf einer Kunststoffplatte. Unterhalb des Motorsockels wurden in der Nähe der vier Ecken vier Federn platziert, die ebenfalls mit Schrauben und Muttern gesichert wurden. Unter jeder Feder brachte ich zur Erhöhung der Reibung auf der Auflagefläche einen Block aus rutschfestem Material an. Abb. 2 zeigt das fertiggestellte System, an dem ich die Messungen durchführte.
Der Anschluss des Motors an einen Wechselrichter erlaubte es mir, die Drehgeschwindigkeit des Rotors zu steuern und die Beschleunigungs- und Verzögerungszeiten zu kontrollieren.
Schwingungsdatenerfassungssystem
Die durch die Drehung des Rotors eines Elektromotors erzeugten Schwingungen haben eine sehr geringe Amplitude, insbesondere wenn sie weit von den Resonanzfrequenzen entfernt sind. Es kann daher sein, dass sie visuell schwer zu erfassen sind. Ich hatte Schwingungsamplituden in der Größenordnung von Zehntelmillimetern unter normalen Bedingungen und in der Größenordnung von einem Millimeter in der Nähe von Resonanzfrequenzen.
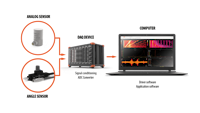
Die von physikalischen Systemen ausgehenden Signale sind analog, während Computer und Rechenmaschinen mit diskreten Zeit- und Amplitudensignalen arbeiten. Aus diesem Grund werden für die Messung und Überwachung Messumformer und Signalverstärker benötigt.
Messumformer sind Geräte, die ein physikalisches Phänomen in ein analoges Signal umformen. Ein Analog-Digital-Wandler (ADC) in einem Verstärker wandelt dieses analoge Signal dann in digitale Daten um, die von der Computersoftware weiterverarbeitet werden.
Unter den verschiedenen Wandlern, die zum Einsatz kommen, sind häufig Beschleunigungssensoren anzutreffen, die Beschleunigungen in ein elektrisches Signal umwandeln. In diesem konkreten Fall verwendete ich IEPE-Sensoren (piezoelektrische Sensoren mit eingebauter Impedanzwandler-Elektronik).
Das Ausgangssignal eines IEPE-Sensors ist ein Spannungssignal mit niedriger Impedanz, während piezoelektrische Sensoren ohne eingebaute Elektronik nur eine elektrische Ladung als Ausgangssignal erzeugen können. Der in einem IEPE-Sensor zur Anwendung kommende Verstärker kann ein Spannungs- oder ein Ladungsverstärker sein.
Darüber hinaus verwendete ich ein von Dewesoft geliefertes robustes KRYPTON-EtherCAT-Datenerfassungssystem. Diese essentielle Komponente half mir in vielerlei wichtiger Hinsicht:
Als Signalverstärker: Das Ausgangssignal der Messumformer ist in der Regel schwach, weshalb ich es vor der Umwandlung in ein digitales Format zusätzlich verstärkte.
Bei der Signalaufbereitung: Der Signalkonditionierer verarbeitet das verstärkte Signal, indem er verschiedene Operationen wie Filterung, zusätzliche Verstärkung und Zeitintegration durchführt.
Als Rekorder: Für mich war der Rekorder nicht unbedingt erforderlich, aber trotzdem praktisch. Das Gerät ermöglichte es mir, experimentelle Daten zu speichern.
Als Analog-Digital-Wandler: Ein ebenfalls nicht unbedingt erforderliches Gerät, das aber häufig eingesetzt wird, da es die Signalverarbeitung mit einem PC ermöglicht. Der Messumformers erzeugt ein kontinuierliches „analoges“ Signal, dessen Wellenform der gemessenen Größe entspricht. Der A/D-Wandler erfasst den Momentanwert des Signals in regelmäßigen Zeitabständen und wandelt ihn in eine diskrete Zahlenfolge, also ein digitales Signal, um. Dieses aus Zahlen bestehende Ausgangssignal kann dann von einem PC verwaltet und verarbeitet werden.
Bei der Analyse rotierender Maschinen wird zur Messung der Drehzahl ein Drehzahlmessumformer (Tachometer) verwendet. Ein solcher Messumformer arbeitet in der Regel entweder optisch oder induktiv.
Ich verwendete den optischen Tachometersensor ICP Laser Tachometer von The Modal Shop. Da es sich um ein IEPE-Gerät handelt, wird es direkt vom Dewesoft KRYPTON gespeist, und es ist keine externe Stromversorgung erforderlich.
Ich befestigte diesen Sensor auf einer angepassten Halterung, die es ermöglichte, ihn auf einen äußerlich am Motorrotor angebrachten Reflexstreifen zu richten. So konnte er zählen, wie oft der Reflexstreifen am laufenden Rotor den Laserstrahl des Tachometers passierte, was mir wiederum ermöglichte, die Drehzahl des Motors zu ermitteln.
Für diesen Vorgang verwendete ich die Funktion Winkelsensor-Mathematik der DewesoftX-Software, mit der sich Impulsfolgen in Drehzahlen umrechnen lassen.
Messungen und Ergebnisse
Beschleunigungsrampen
Als erstes wollte ich in Erfahrung bringen, wie sich das System beim Hochlauf mit verschiedenen Beschleunigungsrampen verhält. Dazu analysierte ich seine Reaktion mit drei verschiedenen Rampen (siehe Abb. 5):
5 Sekunden
10 Sekunden
20 Sekunden.
· 20 Sekunden
Eine Verringerung oder Erhöhung der Anregungsfrequenz wirkt sich auf den Zeitpunkt des Auftretens der Resonanz und auf die Spitzen aus, die die Schwingungen in ihrer Nähe erreichen. Bei weniger steilen Rampen hat das System mehr Zeit, auf die Anregung zu reagieren und die Auswirkungen der Resonanz zu manifestieren. Folglich erreichen die Schwingungen höhere Spitzen.
Bei höheren Geschwindigkeitsgradienten hat das System Mühe, mit der erzwungenen Anregung Schritt zu halten. Da diese viel schneller variiert, hängt die Antwort des Systems immer ein paar Augenblicke zurück. Die Spitzen treten im Vergleich zu niedrigeren Beschleunigungen früher auf und sind weniger stark ausgeprägt.
Da ich mich hauptsächlich für die vertikalen Schwingungen interessierte, platzierte ich den einachsigen IEPE-Beschleunigungssensor so nahe wie möglich an der zentralen vertikalen Achse des Systems.
Zunächst schloss ich die Beschleunigungssensoren an das Krypton-Datenerfassungssystem an und richtete die Software ein. Dann legte ich die Art der Messung (in diesem Fall IEPE) und die Maßeinheit (m/s2) fest und wählte 1 kHz als Abtastfrequenz.
Außerdem musste ich einen Skalierungsfaktor für die Kalibrierung eingeben. Dieser Faktor wird vom Hersteller des Sensors in den Datenblättern als Empfindlichkeitswert vorgegeben, und es reicht aus, ihn in das entsprechende Feld zu kopieren. Abb. 6 zeigt die Schnittstelle für die Konfiguration des Beschleunigungssensors mit Kennzeichnung der genannten Felder.
Nach der Konfiguration des Beschleunigungssensorkanals konnte ich die erforderlichen Daten für jede der drei Geschwindigkeitsrampen erfassen. Abb. 7 zeigt das Systemverhalten bei einer Beschleunigung von 0 auf 1500 U/min in 5 Sekunden.
Die Informationen über die vertikale Position des schwingenden Motors sind am nützlichsten und am einfachsten zu interpretieren. Um sie zu erhalten, führte ich eine doppelte Zeitintegration über die Beschleunigung durch. Die Abb. 8a und 8b zeigen die Konfiguration der doppelten Zeitintegration und ihre Ergebnisse.
Das gleiche Verfahren wendete ich auch auf die 10-Sekunden- und die 20-Sekunden-Rampe an (siehe Abb. 9 und 10).
Wie aus den erfassten Ergebnissen deutlich ersichtlich ist, kommt es in zwei Momenten der Beschleunigungsphase zu einer Verstärkung der Schwingungen. Die Auswirkungen der beiden Resonanzfrequenzen waren für mich viel leichter anhand des Wegsignals zu erkennen als anhand der Beschleunigung.
Nach Ermittlung des Wegsignals wechselte ich vom Zeitbereich zum Frequenzbereich. Dazu verwendete ich die schnelle Fourier-Transformation (FFT). Die FFT ist eine mathematische Methode zur Umwandlung einer Zeitfunktion in eine Frequenzfunktion.
Die FFT zerlegt ein Signal in seine Spektralkomponenten und liefert so Informationen über die enthaltenen Frequenzen. Sie ermöglichte es mir, die Resonanzfrequenzen des Systems zu bestimmen. Die Abb. 11a, 11b und 11c zeigen die FFT für die drei Rampen bei der Spitzenauslenkung, die für die erste der beiden Resonanzfrequenzen aufgezeichnet wurde.
In Tabelle 1 sind die Frequenzen aufgeführt, bei denen sich die Motorschwingungen deutlich verstärkten. Tatsächlich gab es auch noch eine dritte Resonanzfrequenz, die sich jeweils zwischen der ersten und der zweiten manifestierte.
Diese dritte Frequenz verstärkte jedoch horizontale Schwingungen und wurde vom Beschleunigungsmesser nicht ohne Weiteres erkannt. Ich beschloss, sie nicht zu berücksichtigen. Die horizontalen Schwingungen, die ich mit einem parallel zur kurzen Seite der Platte positionierten Messumformer erfasste, waren gering im Vergleich zu den von der dritten Resonanzfrequenz verstärkten.
Bei der ersten Frequenz handelte es sich um eine Wipp-Frequenz, bei der zweiten und dritten um Nick-Frequenzen entlang der beiden Hauptachsen.
| RAMPE | ERSTE RESONANZFREQUENZ Hz/U/min | ZWEITE RESONANZFREQUENZ Hz/U/min |
|---|---|---|
| 5 Sekunden | 8,789 / 527,34 | 19,531 / 1171,86 |
| 10 Sekunden | 8,789 / 527,34 | 19,043 / 1142,58 |
| 20 Sekunden | 8,789 / 527,34 | 19,043 / 1142,58 |
Ordnungsanalyse und Wasserfalldiagramme
Im Anschluss an die Analyse der vertikalen Schwingungen führte ich mit der Analysesoftware DewesoftX eine Ordnungsanalyse an unserem Motor durch. Sie sollte dazu dienen, festzustellen, ob eine Rotorunwucht oder eine andere Systemstörung vorlag, die erkennbar zur Schwingungsverstärkung beitrug.
Wie bereits erwähnt, stehen die Probleme, die in einer rotierenden Maschine auftreten, in engem Zusammenhang mit den Ordnungen, bei denen sie sich manifestieren. Phänomene der Ordnung 1.x in rotierenden Maschinen weisen auf eine Restunwucht hin, die bei realen Motoren immer vorhanden ist, Phänomene der Ordnung 2.x hingegen auf Ausrichtungsfehler zwischen der Antriebs- und der Betriebsmaschine.
Da mein Modell recht einfach und der Motor von jeglicher Last abgekoppelt war, erwartete ich bei der ersten Ordnung die höchste Intensität. Dies würde eine interne Unwucht als Hauptursache für die Vibrationen bestätigen.
Obwohl die DewesoftX-Software zahlreiche Optionen bietet, lässt sich eine einfache Messung wie diese sehr schnell durchführen. Zunächst musste ich dazu den Sensor für die Messung der Rotordrehzahl einrichten. Wie in Abb. 13 zu sehen ist, benutzte ich einen tachometrischen Sensor.
Danach brauchte ich nur noch das Ordnungsanalyse-Modul (OT) aus dem „Setup“-Bereich der DewesoftX-Software. Dort konfigurierte ich die Parameter für die Ordnungsanalyse, wie in Abb. 14 unter Hervorhebung der für uns interessanten Felder dargestellt.
Ich führte eine zweiminütige Auslaufmessung durch und begann mit der Analyse der ersten 16 Ordnungen. Allerdings berücksichtigte ich in den Ergebnissen nur die ersten acht Ordnungen, da sie die signifikantesten Resultate zeigten. Abb. 15 zeigt die Ergebnisse der Ordnungsanalyse.
Die in Abb. 15 dargestellten Diagramme bestätigten meine Erwartung, dass die Ordnung 1.x im Vergleich zu allen anderen die höchste Intensität aufweisen würde. Es handelte sich um ein reales System, und die anderen Ordnungen wiesen anhand der relativ hohen Intensitäten der Ordnungen 2.x und 3.x auf lose Verbindungen, Spiel und Fehlausrichtungen hin.
Fazit
Das Grundanliegen dieser Studie war die Beantwortung einfacher Fragen wie:
Wodurch werden die Schwingungen im Motor-Platte-System verursacht?
Was könnte mit dem System passieren, wenn der Motor auf Höchstgeschwindigkeit läuft?
Die Analyse dieses einfachen Systems erlaubte es mir aber nicht nur, die Hauptursachen für die Verstärkung von Schwingungen in einer rotierenden Maschine zu ermitteln. Ich konnte auch die Auswirkungen beobachten, die sich ergeben, wenn der Motor Resonanzfrequenzen durchläuft.
Schwingungen, die bei Resonanzfrequenzen hohe Werte erreichen, können das System beschädigen und sogar zerstören. Das Verständnis dieser Resonanzfrequenzen ist von wesentlicher Bedeutung, wenn man den Betrieb in der Nähe solcher Bedingungen vermeiden möchte, ermöglicht es den Konstrukteuren aber auch, das ursprüngliche Design durch Anpassungen oder Änderungen zu verbessern.
Die Datenerfassungssysteme von Dewesoft haben sich für diesen einfachen Fall als perfekt geeignet erwiesen. Die Flexibilität der Erfassungsplattform erlaubte es mir, Daten von mehreren Messpunkten gleichzeitig aufzuzeichnen. Die Möglichkeit, Messungen in mehreren Richtungen durchzuführen, ermöglicht zudem sehr komplexe und fortgeschrittene Analysen und reduziert die erforderliche Laborzeit.
Referenzen
Noise and Vibration Analysis; Signal Analysis and Experimental Procedures – A. Brandt – Wiley, 2011.
Vibration-Based Condition Monitoring: Industrial, Aerospace and Automotive Applications – R. B. Randall – Wiley, 2010.