Inhaltsübersicht
Kategorien durchsuchen
Autoren durchsuchen
 AB
ABAlberto Boffi
 AL
ALAlessia Longo
 AH
AHAl Hoge
 AB
ABAljaž Blažun
 BJ
BJBernard Jerman
 BČ
BČBojan Čontala
 CF
CFCarsten Frederiksen
 CS
CSCarsten Stjernfelt
 DC
DCDaniel Colmenares
 DF
DFDino Florjančič
 EB
EBEmanuele Burgognoni
 EK
EKEva Kalšek
 FB
FBFranck Beranger
 GR
GRGabriele Ribichini
Glacier Chen
 GS
GSGrant Maloy Smith
 HB
HBHelmut Behmüller
 IB
IBIza Burnik
 JO
JOJaka Ogorevc
 JR
JRJake Rosenthal
 JS
JSJernej Sirk
 JM
JMJohn Miller
 KM
KMKarla Yera Morales
 KD
KDKayla Day
 KS
KSKonrad Schweiger
Leslie Wang
 LS
LSLoïc Siret
 LJ
LJLuka Jerman
 MB
MBMarco Behmer
 MR
MRMarco Ribichini
 ML
MLMatic Lebar
 MS
MSMatjaž Strniša
 ME
MEMatthew Engquist
 ME
MEMichael Elmerick
 NP
NPNicolas Phan
 OM
OMOwen Maginity
 PF
PFPatrick Fu
 PR
PRPrimož Rome
 RM
RMRok Mesar
 RS
RSRupert Schwarz
 SA
SASamuele Ardizio
 SK
SKSimon Kodrič
 SG
SGSøren Linnet Gjelstrup
 TH
THThorsten Hartleb
 TV
TVTirin Varghese
 UK
UKUrban Kuhar
Valentino Pagliara
 VS
VSVid Selič
 WK
WKWill Kooiker
Testen des Antriebsstrangs bei einem elektrischen Formula-SAE-Rennwagen
Antonio Maria Pisciotta, Agostino Formisano, and Francesco Giuseppe Quilici
E-Team Squadra Corse
September 26, 2025
Das italienische Formula-SAE-Team „E-Team Squadra Corse“ nimmt seit 2008 am Formula-Student-Wettbewerb der SAE teil. Für die Saison 2022/23 hat das Team einen drastischen Wechsel vollzogen: Die bekannten Verbrennungsmotoren wurden durch zwei Axialflussmotoren ersetzt. Die Umstellung des Antriebsstrangs vom Verbrennungsmotor auf einen elektrischen Antrieb erwies sich als anspruchsvolle Herausforderung. Bei der Erfassung, Verarbeitung und Analyse von Testdaten zur Klärung der Auswirkungen dieser Umstellung auf das Verhalten des Fahrzeugs arbeitete das Team mit Dewesoft zusammen.

In der Saison 2023 nahm das E-Team der Universität Pisa eine Änderung vor. Es wechselte von der Verbrennungskategorie in die Elektrokategorie des Formula-Student-Wettbewerbs der SAE. Um diese Änderung zu unterstützen und den Motor zu verbessern, arbeiteten unsere Antriebsstrang- und Elektronik-Teams zusammen. Sie installierten und überwachten alle elektronischen und elektrischen Vorrichtungen des Fahrzeugs. Für den Umstieg auf Elektroantrieb mussten wir den hinteren Teil des Chassis des Einsitzers verändern, um den neuen Antriebsstrang und das Akkupack unterbringen zu können.
Das EV-A-Fahrzeug
Das erste Elektroauto des E-Teams und des Ateneo Pisano heißt E-VA. Es hat ein Hybridchassis. Das Heck besteht aus einem Stahlfachwerk, und die Front aus einem Kohlefaser-Monocoque. Das Antriebssystem des Fahrzeugs umfasst zwei Heckmotoren aus der Luftfahrttechnik. Jeder dieser Motoren ist mit einem Wechselrichter gekoppelt. Diese Konfiguration verbindet die Motoren mit dem Akkupack.
Das E-Team Squadra Corse testete seinen elektrischen Prototyp mit dem Namen ET15: E-VA auf dem Circuito di Siena. Diese internationale Kartbahn befindet sich in Castelnuovo Berardenga, in der Provinz Siena (Toskana, Italien).
| Spezifikationen | Abkürzungen | Numerische Werte |
|---|---|---|
| Masse (Fahrzeug mit Fahrer) | m | 336 kg |
| Schwerpunkthöhe | h | 300 mm |
| Radstand | l | 1530 mm |
| Vordere Spurweite | t1 | 1235 mm |
| Hintere Spurweite | t2 | 1146 mm |
| Achslastverteilung (% vorne) | wb | 45 |
| Rollzentrumshöhe vorne (wankfrei) | q1 | 12 mm |
| Rollzentrumshöhe hinten (wankfrei) | q2 | 34 mm |
| Leistung | Ptot | 74 KW |
Sensorkonfiguration
Die Sensorausstattung des Fahrzeugs umfasst sowohl teameigene als auch von Dewesoft bereitgestellte Sensoren.
Die Sensoren des Teams
Das Team hatte bereits eigene interne Sensoren am Prototyp montiert. Normalerweise statten wir das Fahrzeug aus mit:
einem potentiometrischen Fahrpedalwegsensor (TPS) zur Messung der Stellung des Fahrpedals;
einem mit der Zahnstange verbundenen Lenkwinkelsensor (SPS); zur Berechnung des Lenkwinkels der einzelnen Vorderräder anhand der Lenkbewegungen;
vier Hallsensoren, einem für jede Nabe, zur Messung der Raddrehzahl (ωij) jedes Rades;vier Potentiometern, einem für jeden Stoßdämpfer, zur Messung des Federwegs.
Die Dewesoft-Sensoren
Die externen, von Dewesoft hergestellten und gelieferten Sensoren sind auf dem neuesten Stand der Technik. Im Einzelnen handelt es sich um:
SIRIUS Modular – ein vielseitiges und robustes Datenerfassungssystem mit hochwertigen High-End-Signalaufbereitungsverstärkern für verschiedenste Signal- und Sensortypen;
DDC-CT-Stromwandler – bietet die Vorteile eines Nullflusswandlers, jedoch mit geringerem Stromverbrauch und kompakterem Design;
Stromwandler – hochpräzise Stromzangensensoren für Gleichstrom- und Wechselstrommessungen;
Spannungssensoren
DS-GYRO3 – eine leistungsstarke inertiale Messeinheit (IMU), die fest mit dem Fahrzeugrahmen verbunden und möglichst nahe am Massenschwerpunkt (CoG) positioniert ist und die Beschleunigung in Längs-, Quer- und Vertikalrichtung sowie die Wank-, Nick- und Gierrate am Installationspunkt misst.
Fahrzeugdynamik
Dank der IMU von Dewesoft konnten wir wichtige fahrdynamische Daten erfassen, die normalerweise nur schwer zugänglich sind. Zunächst überprüften wir die Konsistenz und die Vorzeichen der Daten. Abb. 2 zeigt das als Referenz dienende Modell des Fahrzeugs.
Der erste Schritt bestand darin, die Signale der Dewesoft-Hardware mit denen der internen Hardware zu vergleichen.
Wie in Abb. 3 zu sehen ist, war die Erfassung anfangs nicht synchronisiert, was zu einem erheblichen Zeitversatz von 127,6 Sekunden führte. Diese Synchronisation konnte jedoch mithilfe der doppelten Erfassung des Fahrpedalsignals durchgeführt werden, sodass sich die Signale – wie in Abb. 4 dargestellt – überlagerten.
Anschließend überprüften wir die Übereinstimmung der Vorzeichen der Signale. Dazu betrachteten wir Abb. 3 und verglichen ein Referenzsignal mit einem bestimmten Vorzeichen – in diesem Fall den Lenkwinkel – mit einem anderen Signal. Um die Korrektheit der Vorzeichen zu prüfen, betrachteten wir die Ausrichtung von Lenkwinkel, Querbeschleunigung und Gierrate. Abb. 5 zeigt, dass ay und der Lenkwinkel entgegengesetzte Vorzeichen aufweisen, weshalb eine Drehung von ay notwendig war.
Beim Vergleich von Lenkwinkel und Gierrate wurde hingegen – wie in Abb. 6 ersichtlich – festgestellt, dass die Vorzeichen übereinstimmten und somit korrekt waren.
Signalverarbeitung
Zunächst extrapolierten wir eine einzelne Runde aus den erfassten Daten. Diese Extrapolation erfolgte durch numerische Integration der Gierrate. Daraus bestimmten wir die Positionen im Gierwinkelverlauf für die Werte 2π und 4π (siehe Abb. 7).
Wir ermittelten die Trajektorie durch Auswertung der direkt von der IMU abgetasteten Schwerpunktgeschwindigkeiten und Gierrate und Integration der Gleichung (1) zum Erhalt der absoluten x- und y-Daten (siehe Abb. 8).
Mechanische Analyse
Die Entwicklung eines Hochleistungsprototyps erfordert eine eingehende Untersuchung der Fahrzeugdynamik zur Verbesserung der Rundenzeitleistung. Im Laufe der Jahre hat die Technologie zur Entwicklung besserer Fahrzeugmodelle beigetragen. Diese Modelle erlauben es uns, das Verhalten von Fahrzeugen genauer vorhersagen, erfordern jedoch eine Korrelation zwischen Simulations- und tatsächlichen Messdaten. Dank Dewesoft können wir Signale mit einer genaueren Auflösung erfassen.
Fahrzeugmodell
Die Abteilung Fahrzeugdynamik hat verschiedene Fahrzeugmodelle entwickelt. In diesem Fall validierten wir das mit der kommerziellen Software Adams Car entwickelte Mehrkörpermodell. Das Modell in Abb. 9 hat 13 Freiheitsgrade. Diese beziehen sich auf die Bewegungen der gefederten Masse, die ungefederten Massen, das Abrollen der Räder und das Differential.
Ein Fahrzeugmodell gliedert sich in drei Hauptebenen:
Vorlagen (Templates) sind parametrische Modelle, die im Expertenmodus des DewesoftX Template Builder erstellt werden und die Topologie und die wesentlichen Funktionen der Modelle definieren.
Teilsysteme (Subsystems) basieren auf Vorlagen in der DewesoftX Standard Interface und können mittels parametrischer Daten (z. B. Aufhängungskoordinaten) modifiziert werden.
Baugruppen (Assemblies) enthalten alle Subsysteme, die zur Definition des Fahrzeugs erforderlich sind. Sie können auch einen virtuellen Prüfstand umfassen, um standardisierte oder benutzerdefinierte Manöver jeder Art zu simulieren.
Das Team erstellte Vorlagen für jeden Hauptbereich des Fahrzeugs. Dazu gehörten die vordere und hintere Aufhängung, die Lenkung, das Fahrgestell, die Räder, die Bremsen und der Antriebsstrang. Durch Änderung der entsprechenden Parameter, wie der Aufhängungsgeometrie, konnten wir Unterschiede zwischen den Modellen 2023 und 2022 feststellen.
Der erste Schritt bei der Überprüfung unserer Subsysteme bestand darin, festzustellen, ob alle Randbedingungen korrekt angewendet wurden. Anschließend analysierten wir, wie in Abb. 9 dargestellt, einige kinematische Merkmale einer Aufhängungsbaugruppe.
Statische Validierungen
Das Adams-Car-Modell umfasst elastische Verbindungselemente (Buchsen) zwischen den Dreiecksquerlenkern und dem Fahrgestell. Für die Modellierung der Buchse wird in der Adams-Car-Software eine 6x6-Matrix verwendet, wobei sechs generalisierte Auslenkungen und Geschwindigkeiten als Eingaben dienen und einen generalisierten Kraftvektor als Ausgabe erzeugen.
Für dieses Fahrzeug setzten wir die Rotationswerte auf Grundlage des verwendeten Verbindungstyps auf 0. Außerdem nahmen wir für die Buchsen ein isotropes Verhalten an, was bedeutet, dass die verallgemeinerten Kräfte in allen drei Richtungen gleich wirken.
Basierend auf einer Testkampagne mit Dewesoft in den Vorjahren setzten wir Dehnungsmessstreifen ein, um die Verformungen einer Zugstange während eines Zugversuchs zu erfassen. Die Dehnungsmessstreifen waren notwendig, um die Verformung des Lenkers von der der Verbindungsglieder an den Gelenkköpfen zu unterscheiden.
Die Messanordnung war als Halbbrückenschaltung mit zwei weiteren, durch Verstärkung simulierten Widerständen ausgeführt. Diese Anordnung emulierte eine Vollbrückenkonfiguration. Für die statische Testanordnung verwendeten wir einen Pushrod und M6-Kugelgelenke von SKF (siehe Abb. 10). Die Zugstange ist über zwei Klemmbacken und kalibrierte Schrauben zwischen der Klemmbacke und dem Kugelgelenk mit der Maschine verbunden. Zur Datenerfassung diente ein selbstgebauter BNC-Stecker, der an die Kabel des Verstärkersystems gelötet wurde. Die Kalibrierung erfolgte mithilfe eines an eine Maschine montierten Pushrod, den wir als Referenz verwendeten. Nach der Kalibrierung wurden 2 kN aufgebracht.
Die Ergebnisse, die wir erhielten, bezogen sich auf die gesamte Pushrod-Baugruppe, und wir führten eine Interpolation durch (siehe Abb. 11). Dieser Prozess erlaubte es uns, eine .bus-Datei zu erstellen, die in die Software eingegeben werden konnte (siehe Abb. 12).
Dehnungsmessstreifen-Test
Nachdem das Gesetz der elastischen Verbindungen hergeleitet war, analysierten wir die in Zusammenarbeit mit Dewesoft durchgeführten dynamischen Tests. 2022 hatten wir eine Testkampagne durchgeführt, bei der die Aufhängungslenker mit Dehnungsmessstreifen instrumentiert waren. Diese Instrumentierung ermöglichte es uns, alle Belastungen der Aufhängungslenker abzuleiten. Anders als 2024 war das Fahrzeug 2022 mit einem Verbrennungsmotor ausgestattet. Die Fahrzeugdaten sind Tabelle 1 zu entnehmen.
Die Tests bestätigten, dass die von der Software gemessenen Kräfte mit unseren Messungen übereinstimmten. Die Studie betrifft ein Beschleunigungs- und Bremsmanöver. Abb. 13 zeigt einen Vergleich zwischen dem Modell und den Messungen der Längsbeschleunigung und Längsgeschwindigkeit.
Abb. 13 zeigt, dass der kinematische Teil mit dem gemessenen Verhalten übereinstimmt. Einige Oszillationen sind auf Vibrationen und Rauschen während der Datenerfassung zurückzuführen. Abb. 14 zeigt die interne Nomenklatur des Teams zur Definition der von der Aufhängung vorgegebenen Randbedingungen. Mit der Definition der Nomenklatur ist es möglich, die in den folgenden Abbildungen dargestellten Ergebnisse zu interpretieren. Die hier dargestellten Ergebnisse beziehen sich auf die linke Vorderradaufhängung.
Die Ergebnisse zeigen, dass die Kraftverläufe tendenziell genau sind, aber nicht immer perfekt übereinstimmen. Diese Ungenauigkeit ist auf zwei Faktoren zurückzuführen:
Die in der Software modellierte Straße ist eine glatte Ebene.
Die viskose Charakteristik der modellierten Buchse hat einen linearen Verlauf.
Eine eingehendere Untersuchung ihres Verhaltens, die wir zu einem späteren Zeitpunkt durchführen werden, kann ein klareres Bild liefern.
Testkampagne auf der Rennstrecke in Siena
Nach der Testkampagne im Jahr 2022 fuhren wir 2024 mit der Analyse des mechanischen Teils des in Siena durchgeführten Tests fort. In diesem Fall war das Fahrzeug mit einem Elektromotor ausgestattet, dessen Eigenschaften in Tabelle 1 dargestellt sind.
Dank der inertialen Messeinheiten (IMU) vom Typ DS-GYRO3 konnten wir Werte messen, die normalerweise nur schwer zu ermitteln sind. Der Testtag umfasste drei Hauptabschnitte:
ein 4–5 Runden umfassendes Fahrertraining
diverse Kurzläufe (wie AutoX) zur Ermittlung der maximalen Leistung
einen Dauertest über 22 Runden
Zur Validierung zogen wir die siebte AutoX-Runde heran. Wir wollten uns die wichtigsten Messwerte für ein Fahrzeug ansehen. Dazu gehören Beschleunigungen und Geschwindigkeiten auf Fahrzeugebene sowie die Geschwindigkeiten aller vier Räder. Aufgrund von Problemen während der Datenerfassungsphase war es nicht möglich, den Hub der vier Stoßdämpfer auszuwerten. Abb. 17 zeigt die Ergebnisse.
Beim Vergleich der simulierten und gemessenen Werte sind alle Signale konsistent. Geringe Abweichungen gibt es lediglich beim Signal des linken Hinterrads in der Phase, in der das Rad durch die seitliche Belastung angehoben wird. Zur Vervollständigung der Validierungen verglichen wir noch die Signale der Zahnstangenbewegung.
In Abb. 20 ist zu erkennen, dass die Tendenz übereinstimmt, jedoch mit leicht niedrigeren Spitzenwerten. Diese können wir auf eine Reifencharakteristik zurückführen, die die Schräglaufwinkel bei gleicher Vertikallast und Seitenkraft unterschätzt. Diese Unterschätzung könnte durch den nicht idealen Zustand des Asphalts am Testtag bedingt sein.
Trotz geringfügiger Abweichungen konnte das Fahrzeugmodell aufgrund der Testkampagne als validiert angesehen werden, und wir können das Modell nun bei der Entwicklung unserer zukünftigen Fahrzeuge einsetzen.
MAP-Ansatz
Der MAP-Ansatz (Map of Achievable Performance) ermöglicht die Untersuchung der Fahreigenschaften unseres Fahrzeugs.
Idealerweise sind bei einem stationären Fahrmanöver alle zeitlichen Ableitungen – in Längs-, Quer- und Gierbewegung – Null. In der Praxis bedeutet dies, dass das Fahrzeug mit konstanter Längsgeschwindigkeit auf einer Kreisbahn mit konstantem Radius fährt. Durch die Wiederholung dieses Prozesses für verschiedene Längsgeschwindigkeiten lassen sich die erreichbaren Bereiche und die Fahreigenschaften bestimmen.
Das vollständige Modell wird durch die Kombination aller definierten Teilsysteme erstellt. Es wird durch mehrere Manöver aus offenen Lenkeingaben gestartet, darunter auch ein Rampensteuerungsmanöver (siehe Abb. 21). Die Rampe erfolgt langsam und erstreckt sich über einen langen Zeitraum.
A. MAPs β - ρ
Zwei Variablen, der Schwimmwinkel des Fahrzeugs und die seitliche Abweichung des Geschwindigkeitsvektors vom Schwerpunkt, sind als β bzw. ρ definiert, wobei ρ die Krümmung der Schwerpunktbahn im stationären Zustand repräsentiert. Die Gleichungen für die beiden Variablen lauten wie folgt:
Die β-ρ-MAP zeigt das Fahrverhalten des Wagens. In Abb. 22 stimmt die Gierrate r normalerweise mit dem Vorzeichen des Lenkwinkels überein. Dies gilt jedoch nicht für die Quergeschwindigkeit v. Es ist zu beachten, dass sich die Fahrzeugreaktion hier bei konstanter Geschwindigkeit mit einer Änderung der Krümmung umkehrt. Außerdem haben β und ρ bei niedrigen Geschwindigkeiten das gleiche Vorzeichen – ein Verhalten, das oft als Nose-out bezeichnet wird. Mit zunehmender Geschwindigkeit kehrt sich dieser Effekt um und führt zu einem Nose-in-Verhalten.
Andere MAPs helfen, das Konzept des Unter- und Übersteuerns besser zu verstehen.
B. MAPs ρ - δv
Die Fahrzeugdynamik befasst sich mit der Untersuchung des Fahrzeugverhaltens als Reaktion auf die Eingaben des Fahrers. Die ρ-δv-Ebene kann diese Beziehung gut darstellen (siehe Abb. 23).
Es ist ersichtlich, dass einige Kurven konstanter Längsgeschwindigkeit bei zunehmendem Lenkwinkel eine Grenze erreichen. Diese Instabilität kann darauf hindeuten, dass das Fahrzeug zum Untersteuern neigt.
C. Erreichbare Eingangsbereiche
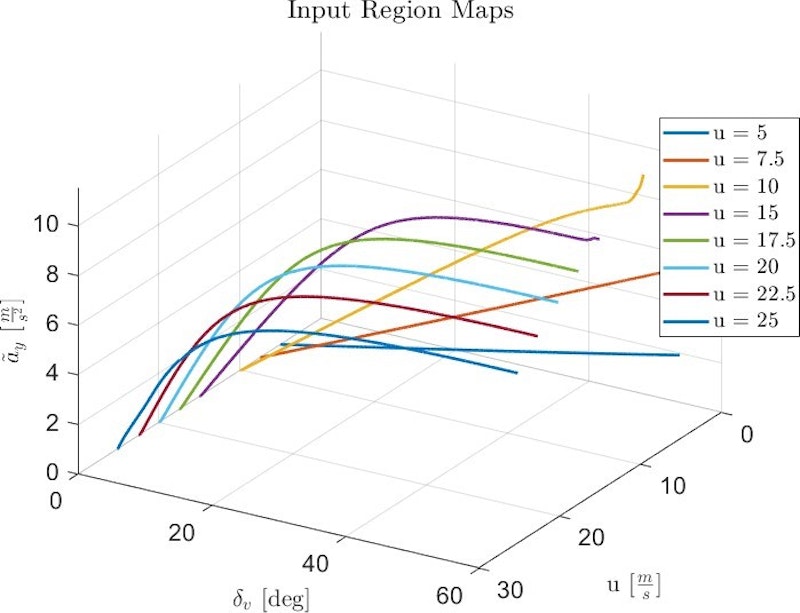
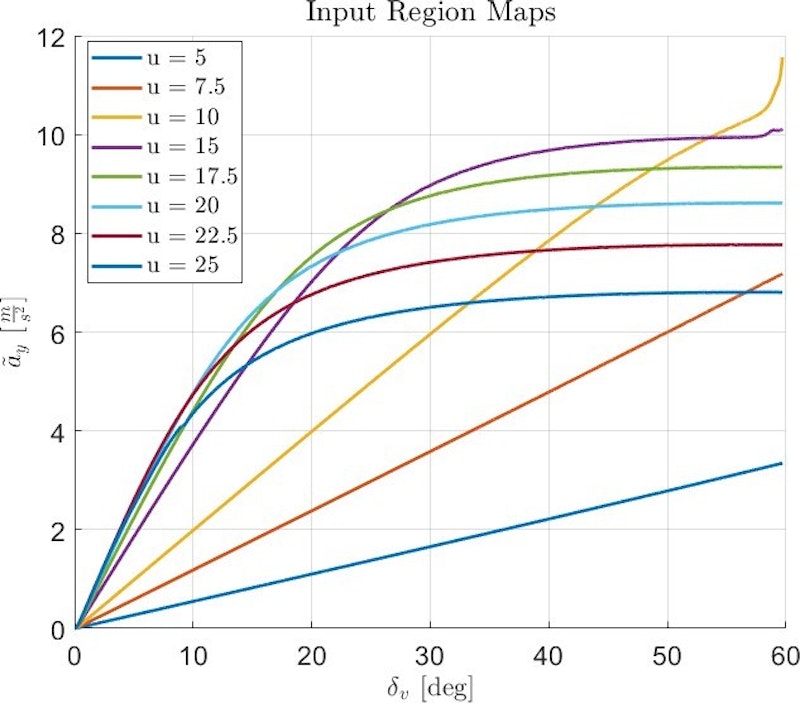
Die Eingangs-MAPs für die Größen u, δv und ãy ermöglichen ein besseres Verständnis der Fahrzeuggrenzen hinsichtlich der erreichbaren Querbeschleunigung. Abb. 24 zeigt die Eingangs-MAPs des Fahrzeugs.
Anhand der Eingangs-MAPs lässt sich erkennen, ob das Fahrzeug zum Übersteuern neigt. Ein solches Verhalten würde bedeuten, dass die Grenze durch die kritische Geschwindigkeit und nicht durch die Haftung bestimmt wird. Da dies hier nicht der Fall ist, bestätigt diese Analyse ein untersteuerndes Verhalten des Fahrzeugs.
Elektrische Analyse
Die Analyse der während des Tests gemessenen elektrischen Größen erlaubte es uns, einige Probleme zu lösen, die das Fahrzeug plagten. Insbesondere hatten wir bei früheren Tests ein abnormales Verhalten festgestellt, das bereits mit bloßem Auge und Ohr wahrnehmbar gewesen war. Während das Fahrzeug normal lief, war es gelegentlich zu Ruckeln und Aussetzern gekommen. Darauf waren kurze Leistungsabfälle gefolgt, bevor das Fahrzeug wieder normal lief.
Das gleiche Verhalten trat auch beim Siena-Dauertest auf. Mithilfe der Tools von Dewesoft konnten wir das Problem jedoch identifizieren und beheben. Dazu isolierten wir zunächst die Momente, in denen die Anomalie auftrat. Auf diese Weise konnten wir die Momentanwerte der vom Motor aufgenommenen elektrischen Leistung vergleichen. Außerdem untersuchten wir das Fahrpedalsignal, die Fahrzeuggeschwindigkeit und die Phasenströme auf der Wechselstromseite. Diese Einstellungen sind in Abb. 25 zu sehen.
Der nächste Schritt bestand darin, die Fahrpedal- und Geschwindigkeitsprofilsignale in den Phasen zu analysieren, in denen das Fahrzeug ein anomales Verhalten zeigte. Abb. 5 zeigt eines der Zeitintervalle, in denen die Anomalie auftrat. Als das Fahrzeug langsamer wurde, reagierten weder Antrieb noch Bremsen wie erwartet. Das Fahrpedalsignal (grün) änderte sich schnell. Diese Änderung erfolgte mit einer zu hohen und ungünstigen Frequenz.
Diese Entdeckung half uns zu erkennen, dass die Anomalie die Fahrzeugmechanik beeinträchtigte, was zu einem Ruckeln des Fahrzeugs führte. Die durch den Fuß des Fahrers induzierte Bewegung bestätigte dies. Nachdem wir dies festgestellt hatten, konzentrierten wir uns darauf, die Ursache des Problems zu finden. Abb. 25 zeigt den Verlauf der drei Phasenströme des Motors. Es ist ersichtlich, dass das Fahrzeug mit dem Abfall der Geschwindigkeit zu ruckeln beginnt und sich die Ströme gegenseitig aufheben.
Dann untersuchten wir den Moment, in dem sich die Ströme gegenseitig aufhoben. Wir stellten fest, dass sie die vom Steuersystem festgelegten Sicherheitsgrenzen überschritten. Abb. 26 zeigt einen Vergleich desselben Signals. Dieses Signal entspricht dem Spitzenstrom, den der Motor aufnimmt. Er wird vom Steuersystem gemessen. Der Vergleich erfolgt mit dem Momentanstrom, der von den analogen Sensoren erfasst wird, wie beispielsweise Iu.
Deutlich zu erkennen sind die unterschiedlichen Werte desselben Signals. Diese wurden mit einem analogen Stromsensor bei 200 kHz gemessen, aber auch mit einer viel niedrigeren Abtastrate durch das Onboard-Telemetriesystem erfasst.
Obwohl sich die Werte vor dem Stromabfall ähneln, gibt es einen entscheidenden Unterschied: Der externe Sensor misst unmittelbar vor dem Abfall über 400 A. Die Onboard-Telemetrie hingegen registriert zum gleichen Zeitpunkt nicht einmal den Spitzenwert.
Als Nächstes brachten wir das Signalfrequenz-Analysetool von DewesoftX zum Einsatz. Wir führten eine schnelle Fourier-Transformation (FFT) der gemessenen Stromsignale, einschließlich des Batterie- und Phasenstroms für die Versorgung des Motors, durch. Unser Ziel war es, den harmonischen Anteil über den gesamten Erfassungsbereich zu untersuchen.
Abb. 27 zeigt oben den Verlauf des Batteriestroms, im mittleren Bereich dessen momentane FFT und unten das Geschwindigkeitsprofil. Rechts ist die GPS-Karte dargestellt. Der Screenshot entspricht den Momenten unmittelbar vor dem Auftreten einer der Anomalien. Auffällig in der momentanen FFT ist das Vorhandensein mehrerer Spitzen mit hoher Amplitude im Spektrum. Harmonische treten bei 12 kHz sowie bei deren Vielfachen, also 24, 36 und 48 kHz, auf. Zudem sind sie auch bei etwa 18 kHz und 20 kHz erkennbar.
Wir analysierten zunächst das Verhalten der Wechselrichter an, deren Schaltfrequenz wir auf 6 kHz einstellten. Die Ansteuerlogik der Wechselrichter zeigt, warum die Harmonischen im Spektrum bei 12 kHz und Vielfachen davon auftreten, was dem Doppelten der verwendeten Schaltfrequenz entspricht.
In unserem Fall handelte es sich um unipolare PWM-Wechselrichter, bei denen die Ausgangsspannung in der durch die Grundschwingung definierten Halbperiode nur positive oder nur negative Werte annimmt. Dieses Verhalten ergibt sich aus der gezielten Ansteuerung der oberen oder unteren Zweigschalter. Im Gegensatz zu bipolaren PWM-Wechselrichtern schließen sich diese Steuerungsmodi nicht gegenseitig aus.
Wie Abb. 28 zeigt, verdoppelt diese Art der Steuerung die Schaltfrequenz im Vergleich zu der üblicherweise angegebenen Frequenz. Diese Verdopplung erklärt, warum die FFT trotz einer eingestellten Frequenz von 6 kHz Harmonische bei 12 kHz und Vielfachen davon zeigt. Zudem ist ersichtlich, dass wir für diese Art der Ansteuerung zwei um 180° phasenverschobene Trägersignale implementieren mussten.
Ein Vorteil dieser Steuerung im Vergleich zur bipolaren PWM liegt in der Reduzierung der Joule-Verluste während der Schaltvorgänge sowie der geringeren elektromagnetischen Interferenz (EMI). Dank der hohen Abtastfrequenz konnten wir unsere vorherigen theoretischen Erkenntnisse zur unipolaren PWM-Steuerung experimentell bestätigen. Tatsächlich sind die Spannungen der drei Phasen in der Halbperiode der Grundschwingung „unipolar“ und um 120° elektrisch phasenverschoben (siehe Abb. 29).
Die Fehlerdiagnose ergab, dass das übermäßige Rauschen der Wechselrichter die Sicherheitsgrenzen für Wechsel- und Gleichströme überschritt. Das interne Sicherheitssystem der Wechselrichter unterbrach bei Überschreitung dieser Grenzwerte sofort die Stromversorgung. Aufgrund einer suboptimalen Vorspannung in der Antriebskette führte dies zu einem spürbaren Ruckeln des Fahrzeugs.
Um das Problem zu beheben, konzentrierte sich das Team auf die Motorsteuerung. Wir passten die Regelungsparameter an und erhöhten vor allem die Schaltfrequenz der Wechselrichter von 6 kHz auf 14 kHz. Bei unipolarer PWM-Steuerung erhöhte sich die Frequenz dadurch von 12 kHz auf 28 kHz. Dies führte zu einer Verlagerung des Oberwellenspektrums in einen Bereich, in dem das Rauschen auf natürliche Weise reduziert wurde. So konnte das Überschreiten der vorgeschriebenen Grenzwerte durch das System verhindert werden, und die Stromausfälle wurden beseitigt.
Die elektrischen Tests in Siena halfen auch, die vom Team im Laufe des Jahres entwickelten Modelle zu validieren. Konkret testeten wir das thermische Modell des Motors EMRAX 188 HV, das die Wicklungstemperatur vorhersagt und so ein besseres Wärmemanagement ermöglicht.
Wir erstellten das thermische Modell durch Implementierung eines thermischen Netzwerks mit konzentrierten Parametern. Dank der vorhandenen physikalischen Symmetrien konnten wir einen der 18 Zähne des Stators untersuchen. Die zentrale Hypothese bestand darin, nur die Verluste in den Statorwicklungen als Wärmequelle zu betrachten. Abb. 30 zeigt das Referenzmuster eines der Zähne.
Mit Hilfe des Knotenpotentialverfahrens konnten wir das folgende Matrixgleichungssystem aufstellen:
Dabei ist T der Vektor der Knotentemperaturen und u der Vektor der Eingänge (Temperatur des in den Motor eintretenden Kühlwassers und vom Motor aufgenommener Strom im Effektivwert):
A, B und C sind Matrizen, die die in Abb. 30 dargestellten Schaltungsparameter enthalten. Zusätzlich wird im Modell der elektrische Widerstand (von dem die Verluste durch den Joule-Effekt abhängen) als Funktion der Temperatur gemäß folgender Beziehung aktualisiert:
Durch die Messung des während des Tests aufgenommenen Stroms war es möglich, das entwickelte Modell zu validieren. Abb. 31 zeigt die Temperaturverläufe des motorinternen Sensors sowie die vom Modell für den gesamten Testverlauf, einschließlich der Pausen, geschätzte Temperatur.
Der mit den Dewesoft-Tools durchgeführte Test ermöglichte es uns, das thermische Modell des Elektromotors zu validieren. Zudem zeigte er Bereiche auf, die verbessert werden müssen. Dazu gehören die Genauigkeit der Parameter und eine eingehendere Analyse einiger Elemente. Die Eisenverluste und Magnetverluste haben wir einstweilen genauso vernachlässigt wie das Schätzen der Temperatur der Magnete.
Fazit
Der Test in Siena hat uns wertvolle Einblicke in die elektrische und mechanische Leistungsverhalten des Fahrzeugs gegeben und uns geholfen, ein wichtiges Zuverlässigkeitsproblem zu lösen.
Anhand der Daten konnten wir zudem unsere elektrischen und mechanischen Modelle validieren. Dabei identifizierten wir sowohl Stärken als auch Verbesserungspotenziale, was hilfreich bei der Planung unserer nächsten Schritte ist.
E-Team Squadra Corse dankt Dewesoft, und besonders Nomi, herzlich für die umfassende Unterstützung – von der Bereitstellung der Messtechnik bis zur Auswertung der Ergebnisse.