lunes, 5 de mayo de 2025 · 0 min read
Optimización del desempeño de hidroalas mediante análisis modal y amortiguamiento resonante piezoeléctrico
Para optimizar el comportamiento dinámico de las hidroalas, los investigadores han recurrido al amortiguamiento resonante piezoeléctrico. Esta técnica consiste en realizar un análisis modal detallado de la estructura de la hidroala y posteriormente ajustar el sistema a una frecuencia natural específica mediante el uso de inductores. El montaje experimental emplea parches piezoeléctricos para controlar la flexión y la torsión, y mide las funciones de respuesta en frecuencia (FRF) tanto en condiciones de circuito abierto como de cortocircuito.
¿Qué son las hidroalas?
Las hidroalas funcionan de manera similar a los perfiles aerodinámicos. Son alas o superficies perfiladas instaladas debajo del casco de una embarcación para generar sustentación a medida que el vehículo se desplaza en el agua. Al elevar el casco fuera del agua, las hidroalas reducen la resistencia hidrodinámica, permitiendo que la embarcación alcance mayores velocidades y mejore su eficiencia en el consumo de combustible.
La aplicación del amortiguamiento resonante piezoeléctrico en una hidroala tiene como objetivo mejorar su desempeño dinámico mediante la integración de materiales piezoeléctricos para controlar la flexión y la torsión. Este enfoque innovador permite optimizar el amortiguamiento de vibraciones, ofreciendo avances significativos para la ingeniería marina y aeronáutica.
A través de una serie de sesiones de laboratorio, buscamos realizar un análisis modal detallado y diseñar inductores pasivos. Asimismo, implementaremos circuitos de derivación resonante para reducir las vibraciones de una hidroala de referencia basada en un perfil NACA.
Proceso del experimento
En el Laboratorio de Mecánica Estructural y Sistemas Acoplados del CNAM (Conservatoire National des Arts et Métiers), aplicamos tres etapas para estudiar el amortiguamiento resonante piezoeléctrico implementado en una hidroala.
El primer paso crucial consiste en realizar un análisis modal de la estructura.
El segundo paso implica proponer varias soluciones potenciales para sintonizar la estructura a una frecuencia natural específica.
El tercer paso es validar el resultado de la respuesta en frecuencia tras la implementación del inductor en el circuito.
Análisis modal de la hidroala
La hidroala cuenta con dos parches piezoeléctricos para controlar la flexión en un lado y un parche adicional en el otro lado para controlar la torsión. En este montaje experimental, utilizamos uno de los dos parches de "flexión" como excitación de entrada y el segundo parche de "flexión" como sensor de salida. La entrada consiste en una señal de voltaje de excitación, mientras que la salida es el voltaje medido a través de los electrodos del parche sensor.
Durante el experimento, medimos las funciones de respuesta en frecuencia (FRF) tanto en condiciones de cortocircuito como de circuito abierto, observando que el comportamiento dinámico de la placa varía debido a la influencia de los parches piezoeléctricos.
El tipo de excitación seleccionado para este experimento es el "chirp". Esta elección se basó en el hecho de que una señal chirp puede abarcar un amplio rango de frecuencias, lo que permite estudiar la respuesta en frecuencia de la estructura a lo largo de un extenso rango utilizando una única excitación.
Una señal chirp es un tipo de señal cuya frecuencia aumenta o disminuye progresivamente con el tiempo. Este tipo de señal se utiliza comúnmente en aplicaciones como radar, sonar, comunicaciones y pruebas de vibraciones, ya que permite medir la respuesta de un sistema en un amplio rango de frecuencias. El barrido continuo de frecuencias bajas a altas (o de altas a bajas) hace que las señales chirp sean especialmente efectivas para identificar cómo diferentes frecuencias afectan un sistema o entorno.
Lista de hardware y software de adquisición de datos
Para la adquisición y análisis de datos, utilizamos:
DEWE-43: Es un sistema de adquisición de datos USB de 8 canales, versátil y de tamaño compacto. El dispositivo de mano cuenta con ocho entradas analógicas universales, ocho entradas digitales/contador/encoder y dos entradas de bus CAN de alta velocidad.
DewesoftX: DewesoftX es un software de adquisición de datos y procesamiento de señales utilizado para la medición de señales, registro de datos, procesamiento y visualización en una amplia variedad de aplicaciones de prueba y medición en todos los sectores.
Se obtuvieron dos grupos de datos de funciones de respuesta en frecuencia (FRF) al desconectar y conectar los dos electrodos del parche de "torsión", correspondientes a las condiciones de circuito abierto y de cortocircuito, respectivamente. Estudiaremos dos picos de vibración:
El primer modo de vibración (flexión) ocurre aproximadamente a una frecuencia de 98 Hz.
El segundo modo (torsión) aparece aproximadamente a 520 Hz.
Para obtener un análisis más detallado del segundo modo, extraímos los datos de la FRF en el rango de 500 a 540 Hz. La Figura 2 muestra los resultados obtenidos para las condiciones de cortocircuito y circuito abierto.
Después de medir los datos de FRF, fue necesario calcular la capacitancia piezoeléctrica. Para evitar la influencia de las formas modales, la medición de la capacitancia se realizó a una frecuencia alejada de los modos 1 y 2. La capacitancia medida a 1000 Hz fue de 13.62 nF, utilizando un medidor de capacitancia.
Posteriormente, para encontrar el valor exacto de la frecuencia natural del modo 2, implementamos el método de Polinomios de Fracción Racional (RFP, por sus siglas en inglés) y analizamos los datos obtenidos en DewesoftX.
Al ejecutar el RFP y utilizar funciones ortogonales, obtuvimos el ajuste de curvas y los resultados de frecuencias naturales. Las Figuras 3 y 4 muestran la FRF sintetizada mediante el método RFP tanto para el caso de cortocircuito como de circuito abierto, reproduciendo correctamente las FRF experimentales.
En el siguiente paso, podemos extraer las frecuencias angulares naturales en condiciones de cortocircuito y circuito abierto mediante la siguiente relación:
Por lo tanto, podemos determinar la inductancia LLL y la resistencia RRR óptimas requeridas utilizando las ecuaciones.
Frecuencia natural (cortocircuito) = 518.4547 Hz
Frecuencia natural (circuito abierto) = 520.4007 Hz
Frecuencia angular natural (cortocircuito) = 3.2575 × 10³ rad/s
Frecuencia angular natural (circuito abierto) = 3.2698 × 10³ rad/s
Factor de acoplamiento = 8.67% Inductancia = 6.9 H. Resistencia = 2388.5 Ω
El factor de acoplamiento revela la diferencia entre las condiciones de cortocircuito y circuito abierto. La placa responde a una frecuencia ligeramente mayor cuando se encuentra en condición de circuito abierto que en cortocircuito. Esta variación indica que las condiciones de frontera eléctricas influyen de manera significativa en las vibraciones mecánicas de la hidroala.
Diseño y fabricación del inductor pasivo
Como se muestra en la Figura 5, la estructura de un inductor pasivo consta de cuatro partes: núcleo, carrete, bobina y abrazaderas. En esta sesión, el tipo de núcleo utilizado es RM (de TDK Electronics), y la bobina está hecha de alambre de cobre.
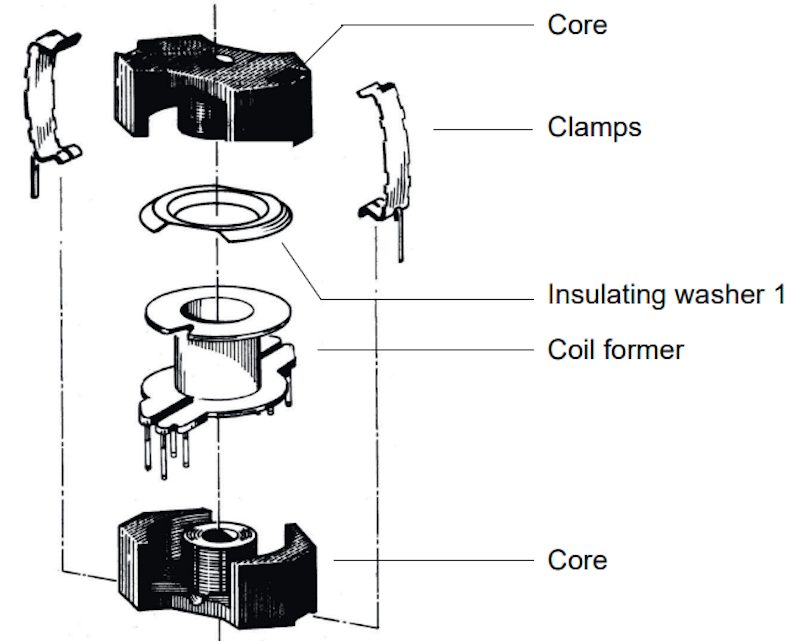
Después de conocer la estructura, nos enfocamos en la inductancia, la resistencia y el factor de llenado del inductor. El valor de la inductancia depende directamente del número de vueltas y de la permeancia del circuito magnético, la cual se obtiene a partir de la fórmula que utiliza ALA_LAL como la permeancia y NNN como el número de vueltas. \(A_L\) como la permeancia y N como el número de vueltas.
En nuestro caso, la inductancia es de 6.9 H. Los datos proporcionados por TDK Electronics indican el valor de la permeancia. Cada tipo de núcleo RM tendrá varios valores de permeancia diferentes. Podemos obtener el número de vueltas utilizando la fórmula correspondiente.
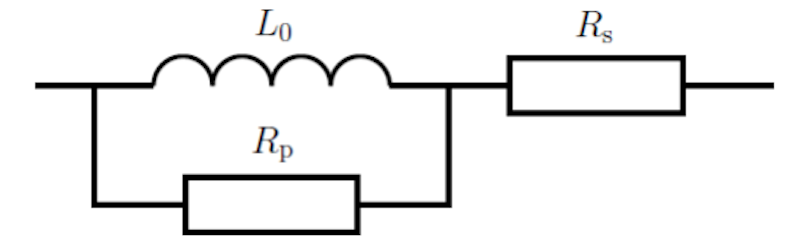
En segundo lugar, \(RS\) (resistencia en serie) modela las pérdidas por efecto Joule en el alambre de cobre, y\(R_p\) (resistencia en paralelo) modela las pérdidas en el hierro del circuito magnético, como se muestra en la Figura 5. En este caso, se desprecia la resistencia en paralelo, y entonces se define la resistencia como:
\(\rho\) es la resistividad del cobre, cuyo valor es 17.2 µΩ.mm. 𝑙𝑁 es la longitud del alambre, determinada por los diferentes tipos de núcleos \(S_{\omega}\) es la sección transversal del alambre. Posteriormente, se introduce el factor de llenado,
Donde \(A_N\) es el área de la sección transversal del devanado, la cual depende del carrete. Dado que el factor de llenado generalmente es de aproximadamente 0.5, este valor ayuda a definir un diámetro de alambre adecuado. La resistencia también puede calcularse mediante:
\(AR\) también depende del tipo de carrete. Si realizamos el cálculo, \(RS\) and \(R_CU\) deberían arrojar resultados similares.
En el siguiente paso, calculamos el diámetro correspondiente al tipo de núcleo utilizado para fabricar el inductor. Podemos utilizar el código de Matlab mostrado en la Figura 6 para estimar el número de vueltas, el área de la sección transversal, la resistencia en serie, la resistencia \(R_CU\), y, finalmente, el diámetro del alambre. En este caso, el cálculo de \(RS\) y \(R_CU\) se realiza para verificar si ambas fórmulas son equivalentes.
El objetivo es encontrar una solución que podamos fabricar considerando el diámetro de los alambres de cobre disponibles:
La primera solución utiliza un núcleo RM14, material sin entrehierro PC200. En este caso, la resistencia en serie teórica es de 75.28 Ω, y la resistencia utilizando un alambre de cobre de 0.2 mm de diámetro es de 70.84 Ω.
La segunda solución emplea un núcleo RM12, material sin entrehierro N87 (o N97). Aquí, la resistencia en serie teórica es de 37.30 Ω, y la resistencia utilizando un alambre de cobre de 0.2 mm de diámetro es de 38.04 Ω.
La tercera solución consiste en utilizar dos inductores RM10 ya disponibles, con inductancias de 1.5 H y 6.0 H, y resistencias de 72 Ω y 325 Ω, respectivamente. Esta solución ofrece una resistencia elevada relevante y puede combinarse con dos resistencias de 1000 Ω para ajustar la resistencia óptima requerida por la derivación resonante previamente definida.
Implementación de derivaciones resonantes en modo simple
Implementamos la solución utilizando los dos inductores y estudiamos varias respuestas en frecuencia en diferentes casos. El objetivo es, primero, obtener la respuesta en frecuencia alrededor de la segunda frecuencia natural de la hidroala sin inductores. Posteriormente, se añaden los inductores al circuito y se comparan los resultados. Finalmente, realizaremos varios ajustes en la resistencia y la inductancia para adecuarnos a los parámetros óptimos obtenidos previamente.
Primero, medimos la respuesta en frecuencia sin inductores mediante una FRF de voltaje/voltaje en el rango de frecuencias de [470, 570] Hz. Este resultado se utilizará como referencia para la comparación después de conectar los inductores.
Posteriormente, implementamos el circuito con inductores, donde la inductancia total es de 1.5 H + 6.0 H = 7.5 H y la resistencia total es de 72 Ω + 325 Ω = 397 Ω.
Luego, obtenemos los datos de respuesta en frecuencia (voltaje/voltaje) tanto sin inductores como con inductores.
Consulta el resultado en la Figura 7, representado mediante un gráfico de Matlab.
El resultado de la respuesta en frecuencia original es satisfactorio, ya que podemos observar claramente el pico de resonancia en la figura. Asimismo, se aprecia el efecto significativo de la derivación resonante, gracias a la FRF obtenida con el inductor.
Sin embargo, estos resultados son difíciles de interpretar, ya que utilizar el voltaje como señal de salida puede generar dificultades al evaluar si la sintonización de la derivación es adecuada. Por esta razón, en los experimentos siguientes, se utiliza la aceleración como salida para estudiar con mayor detalle el comportamiento dinámico de la estructura.
Después de añadir un acelerómetro al montaje experimental, se obtienen nuevos datos de respuesta en frecuencia, los cuales se muestran en las Figuras 8 y 9.
Estas dos figuras indican que los inductores redujeron significativamente la amplitud de vibración de la estructura en torno a la segunda frecuencia natural. No obstante, la resistencia total de los inductores es inferior a la resistencia objetivo, que es de 2388.5 Ω.
Utilizamos Matlab para graficar los datos exportados desde el software DewesoftX y realizar la comparación de resultados.
Se añadieron dos resistencias adicionales de 1000 Ω para aproximarse a la resistencia óptima. La Figura 10 muestra los resultados en los siguientes tres casos: 1) sin inductor, 2) con inductores pero sin resistencias añadidas en serie, 3) con 2000 Ω en serie con los inductores.
Si la resistencia del circuito no se aproxima al valor óptimo, la respuesta de la estructura presenta dos picos de altura media. Tras añadir la resistencia adicional, la resistencia total del circuito se convierte en 397 Ω + 2000 Ω = 2397 Ω, valor que se acerca al valor óptimo de 2388.5 Ω.
Con la resistencia óptima, la respuesta dinámica se minimiza en un rango amplio de frecuencias en comparación con el caso con 397 Ω.
Se añadió resistencia adicional para estudiar cómo afecta la resistencia a la FRF. Además, se observa que los dos picos en el caso de resistencia óptima no están alineados sobre la misma línea horizontal. Es posible mejorar esta condición realizando un ajuste en el valor de la inductancia.
En el siguiente paso, comparamos los casos de resistencia óptima (R), resistencia excedente (R adicional) y resistencia e inductancia óptimas (R y L). La Figura 11 muestra que agregar resistencia adicional recrea el pico en el rango de la frecuencia natural. También observamos que el valor de la inductancia puede afectar el equilibrio de altura entre los dos picos de la respuesta en frecuencia.
Conclusión
La derivación resonante puede mejorar significativamente el comportamiento dinámico de la estructura alrededor de un modo específico. Podemos mejorar el desempeño del amortiguamiento utilizando la inductancia y la resistencia adecuadas, que estén cercanas a los valores óptimos calculados teóricamente.
El efecto de la resistencia puede impactar la altura de los picos: un valor inferior al óptimo resulta en dos picos más altos, mientras que un valor superior al óptimo recrea un solo pico.
Finalmente, el valor de la inductancia puede afectar el equilibrio entre los dos picos. Estas posibilidades de ajuste ofrecen grandes perspectivas para la mitigación de vibraciones en estructuras mecánicas en diferentes aplicaciones, incluyendo hidroalas o aeroalas sometidas a excitaciones por flujo.