miércoles, 10 de mayo de 2023 · 0 min read
La Guía Inigualable para el Análisis en Frecuencia (FFT)
En este artículo, aprenderá sobre FFT y el análisis en frecuencia con suficiente detalle para:
Comprender qué es el análisis FFT y para qué se utiliza
Descubrir cómo se realiza el análisis FFT
Ver cómo funciona el análisis FFT
Introducción al análisis FFT
Conozca qué es el análisis FFT, sus aplicaciones y otros datos interesantes.
¿Qué es el análisis FFT?
El análisis FFT es una de las técnicas más utilizadas al realizar análisis de señales en varios dominios de aplicación. FFT transforma señales del dominio del tiempo al dominio de la frecuencia. FFT es la abreviatura de Fast Fourier Transform.
Con el análisis FFT, se pueden determinar particularidades de una la señal en mucha mayor medida que cuando se inspeccionan los datos del dominio del tiempo. En el dominio de la frecuencia, las características de la señal se describen mediante componentes de frecuencia independientes, mientras que el dominio del tiempo se describe mediante una forma de onda que contiene la suma de todas las características.
Aplicaciones de los analizadores FFT
La inspección de datos medidos en el dominio de la frecuencia es a menudo la parte principal del análisis y monitoreo de señales. Los datos de una variedad de sensores se utilizan en prácticamente todas las industrias para resolver problemas, optimizar diseños, probar prototipos, monitorear maquinaria y muchos otros trabajos como los que se enumeran a continuación:
Monitoreo predictivo del estado de la máquina
Análisis dinámico estructural
Análisis de durabilidad y fatiga
Maquinaria rotativa, detección de fallas en rodamientos, análisis torsional
Análisis de combustión
Pruebas de vibración en el cuerpo humano
Acústica de recintos, diseño de altavoces, análisis de ruido ambiental
Pruebas de respuesta a impactos mecánicos, pruebas de caída
Por ejemplo, cuando se realizan diagnósticos de maquinaria rotativa, ciertos componentes en frecuencia se relacionan con partes específicas dentro de la máquina. Cambiar los niveles de amplitud espectral a lo largo del tiempo puede determinar qué partes, como engranajes y cojinetes, requerirán de mantenimiento... y cuándo.
Además, en entornos acústicamente ruidosos, el análisis FFT se puede utilizar para medir la presión sonora. Descubrir qué intervalos de frecuencia críticos y componentes tonales emergentes están contenidos en el ruido permite a los ingenieros tomar medidas para atenuarlos.
Al realizar pruebas de vibración de componentes y dispositivos, el análisis FFT permite a los ingenieros inspeccionar cómo reaccionan los dispositivos a frecuencias individuales. Esto significa que los espectros en frecuencia pueden ayudar con las optimizaciones de diseño, así como con la especificación de limitaciones de deflexión/distorsión. Los espectros FFT también se pueden usar para determinar curvas de tolerancia aceptables en el intervalo de frecuencia medido y alertar a los usuarios cuando exceden los niveles críticos de vibración en frecuencias específicas.
Resultados de los analizadores FFT
Cuando los analizadores FFT producen datos en el dominio de la frecuencia, los resultados de salida son espectros en frecuencia. Estos espectros normalmente se extraen en una forma denominada espectros de potencia y espectros de potencia cruzada (consulte la referencia 7.1).
Los pasos necesarios para obtener espectros de potencia y espectros de potencia cruzada (PSD, Power Spectral Density) se ilustran en la siguiente imagen:
El primer paso es muestrear los datos de tiempo de entrada en bloques de tiempo FFT. Los datos de tiempo de entrada pueden ser señales de sensor sin procesar o señales preprocesadas (por ejemplo, filtradas). Cada bloque de tiempo tendrá una duración de tiempo \(T\) que se relaciona con la resolución espectral de los espectros. Los bloques de tiempo se pueden configurar para que se aplique una función de ventana y se superpongan.
A continuación, los bloques de tiempo FFT se transforman del dominio del tiempo al dominio de la frecuencia mediante el algoritmo FFT. Cada bloque de tiempo dará como resultado un espectro FFT complejo instantáneo.
Los espectros FFT complejos instantáneos se utilizan para calcular los espectros de potencia instantáneos. Los espectros de potencia se promedian durante un número específico de espectros o una duración de tiempo. Los espectros de potencia tienen valores reales y se relacionan con una señal de entrada. Los espectros de potencia cruzada tienen valores complejos y se relacionan con dos señales de entrada.
El algoritmo de transformación para espectros FFT complejos instantáneos se basa en la formulación DFT (transformada discreta de Fourier), que se puede describir como:
donde \(tn\) son muestras de tiempo discreto, \(fk\) ison muestras de frecuencias discretas,\(N\) es el número de muestras en un bloque de tiempo FFT y la multiplicación de \(1/N\)es el factor de normalización (ver referencia 5.3).
Los cálculos para obtener espectros de potencia instantánea y espectros de potencia cruzada a partir de espectros FFT instantáneos \(A(f)\) y \(B(f)\) e describen a continuación.
Para cada componente en frecuencia, los espectros FFT tienen un valor de amplitud y fase que se puede expresar en coordenadas polares mediante:
Los espectros de potencia y los espectros de potencia cruzada se calculan luego como el producto geométrico de dos espectros FFT:
En consecuencia, la amplitud es el producto de las dos amplitudes espectrales de FFT y la fase es la diferencia entre las dos fases espectrales de FFT (consulte la referencia 4.1).
Estos espectros de potencia luego se promedian sobre un número específico de espectros o una duración de tiempo específica.
La letra \(S\)se usa normalmente para la forma de espectros de potencia bilaterales, como en la forma del espectro FFT complejo original. En la forma de dos caras, el eje en frecuencia va desde \(-f_N\) hasta \(f_N\), donde\(f_N\) es la frecuencia de Nyquist. La frecuencia de Nyquist se describirá en la sección Influencia de la frecuencia de muestreo.
Más comúnmente, se usa la forma de espectro unilateral, que a menudo se denomina con la letra \(G\) y se define como se muestra en la siguiente figura:
Finalmente, se pueden obtener los espectros de potencia unilateral y los espectros de potencia cruzados. El proceso utilizado para obtener tales espectros se realiza normalmente de forma automática en los analizadores FFT.
Otros datos de FFT
Como se mencionó, el análisis de Fourier transforma señales del dominio del tiempo al dominio de la frecuencia. Pero más correctamente, el análisis FFT es un método matemático para transformar una función de tiempo finito \(a(t)\) de \(N\) muestras de tiempo igualmente espaciadas en una función de frecuencia \(A(f)\) de \(N\) muestras de frecuencia complejas igualmente espaciadas (ver referencia 5.3).
De hecho, la transformada FFT no tiene que procesar funciones de muestras de tiempo igualmente espaciadas, sino que también puede procesar muchos otros tipos de N muestras igualmente espaciadas. Por ejemplo, en análisis de orden de maquinaría rotativalas estarán igualmente espaciadas con respecto al ángulo de rotación. La transformación FFT de dichas funciones de análisis de orden creará espectros FFT donde las líneas espectrales no están relacionadas con períodos sinusoidales por segundo [Hz] sino con períodos sinusoidales por revolución cíclica [orden]. Puede encontrar más información sobre el análisis de orden aquí: Análisis de Orden de Dewesoft.
La transformada rápida de Fourier FFT es un desarrollo de la transformada discreta de Fourier (DFT) donde la FFT elimina los términos duplicados en el algoritmo matemático para reducir el número de operaciones matemáticas realizadas. De esta forma, es posible utilizar un gran número de muestras de tiempo sin comprometer la velocidad de la transformación. El número total de multiplicaciones complejas requeridas por FFT es del orden de \(N/(\log_2(N))\), mientras que para DFT es \(N^2\), donde \(N\) es el número de muestras de tiempo involucradas (ver referencia 4.1).
Cómo comenzar a utilizar el análisis FFT
Para comenzar con el análisis FFT, se deben adquirir datos de tiempo. Estos datos pueden haber sido recopilados antes o durante el análisis FFT.
Equipo requerido
Los sistemas DAQ (sistemas de adquisición de datos) se utilizan normalmente para el análisis FFT para adquirir datos en el dominio del tiempo de los sensores. Los datos de los sensores se digitalizan para que puedan ser manipulados y analizados por una computadora y un software. Los sensores junto con un sistema DAQ dedicado conectado a una PC con software de análisis FFT suelen ser la configuración preferida. Es el convertidor de analógico a digital (ADC) del sistema DAQ el que especifica la frecuencia de muestreo �� de las señales.
Los analizadores FFT pueden analizar señales digitalizadas de todo tipo de sensores. Dependiendo de la aplicación, normalmente se utilizarán diferentes tipos de sensores. Por ejemplo, al realizar mediciones acústicas y de ruido, se utilizarán sensores de presión sonora, y para diagnósticos de máquinas y mediciones estructurales, normalmente se utilizan acelerómetros.
Con grandes demandas de optimización de productos con respecto a, p. durabilidad, eficiencia, tiempo de fabricación y seguridad, existe una tendencia creciente hacia la medición de múltiples tipos de cantidades físicas al mismo tiempo. El uso de múltiples tipos de sensores permite la investigación de la correlación entre diferentes parámetros. Por ejemplo, cuando se analizan las mediciones de un motor, a menudo se desea ver cómo se relacionan la vibración, la velocidad, la temperatura y el ruido.
Más información sobre sensores:
Se debe instalar una aplicación de software de análisis FFT en la PC conectada al sistema DAQ. Cuando se ha configurado el sistema y se están ejecutando las mediciones, el usuario puede concentrarse en el software de análisis FFT para completar las tareas de prueba, análisis e informes. Todos los ajustes que definen los resultados espectrales de FFT se gestionan en el software de análisis FFT y se describen en las secciones Ajustes básicos para el análisis FFT y Funciones adicionales utilizadas con el análisis FFT.
Según la configuración del sistema y las limitaciones del proveedor del sistema, los sistemas DAQ con análisis FFT pueden admitir entre 1 y +1000 sensores y, a menudo, brindan una gran lista de funciones de análisis adicionales junto con funciones de almacenamiento, exportación e informes.
En algunas situaciones en las que solo se miden uno o unos pocos sensores, los analizadores FFT portátiles más pequeños pueden ser una mejor opción que los sistemas más grandes. Sin embargo, las características de FFT pueden reducirse en estos sistemas pequeños y es posible que se requieran más pasos manuales para completar el análisis y Los resultados.
Obtenga más información sobre los sistemas DAQ:
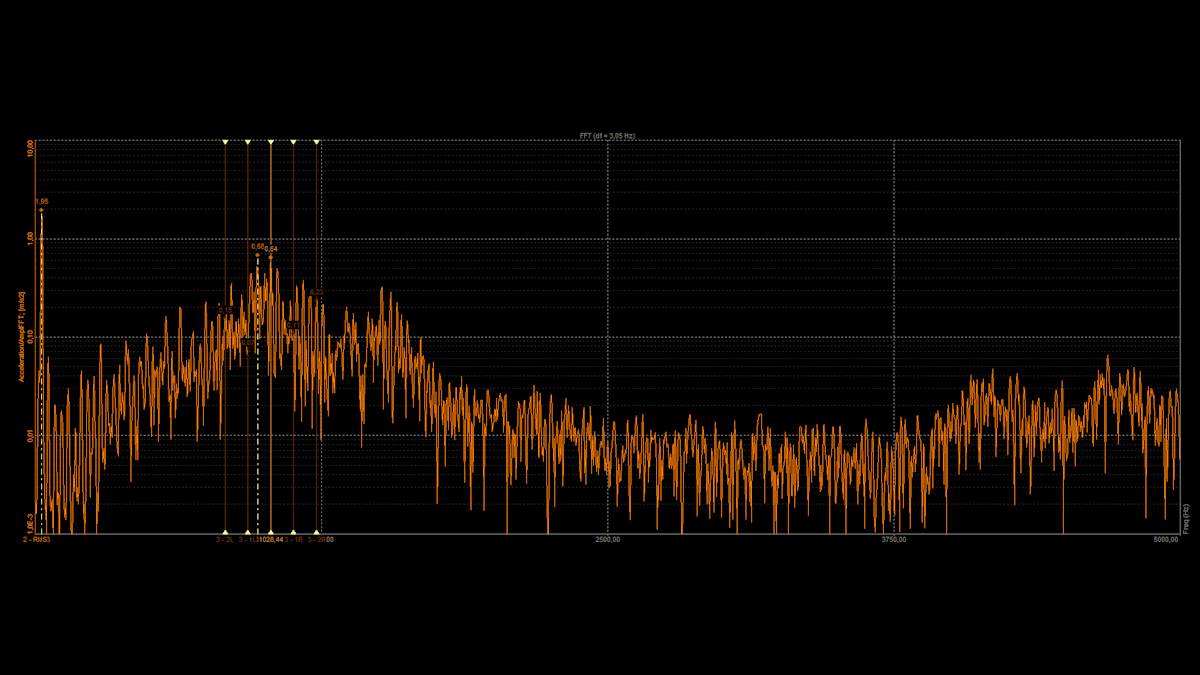
Resolución Espectral
La resolución espectral determina el espacio entre líneas en frecuencia (también llamado resolución de línea) en los espectros producidos. Cuanto mayor sea la resolución espectral, más líneas de frecuencia se incluirán en los espectros de salida del análisis de frecuencia. (A veces, las "líneas" se denominan "intervalos" de frecuencia).
Normalmente, la resolución espectral se puede ajustar a través de uno o más de los parámetros establecidos dependientes que se enumeran a continuación:
Número de Líneas
El número de líneas (\(N\)) indica cuántas líneas se incluirán en los espectros producidos (esto también se relaciona con la resolución espectral).
Resolución de línea, espacio entre líneas y frecuencia delta (\(df\))
El espaciado de línea, ancho de resolución de línea (también conocido como \(f\) o \(\beta\)) indica el ancho de frecuencia entre líneas espectrales vecinas, el intervalo de línea de frecuencia.
Para el análisis de banda base FFT en todo el rango de frecuencia de la señal, la resolución de línea depende de la frecuencia de muestreo (\(f_S\)) la cantidad de líneas. Esto puede ser determinado por:
Para el análisis ampliado o de banda base FFT sobre un intervalo de frecuencia seleccionado, el espacio entre líneas se puede determinar mediante la relación entre el intervalo de frecuencia y el número de líneas dentro de ese intervalo:
Duración del Bloque de Tiempo
También conocida como "duración del bloque", indica la duración de los datos de tiempo que cada espectro requiere que se realice con una determinada resolución de línea.
Cuanto mayor sea la resolución espectral, mayor debe ser la longitud del bloque de tiempo.
La longitud del bloque de tiempo a menudo se denomina \(T\), y está relacionada con la resolución de la línea por:
Por ejemplo, una resolución de línea de 0,5 Hz requiere 2 segundos de datos de tiempo para cada espectro, y la tasa de actualización del análisis FFT será de 2 segundos por espectro.
Nota: se puede usar una función comúnmente conocida llamada superposición para aumentar la tasa de actualización.
Influencia de la Frecuencia de Muestreo
La frecuencia de muestreo o \(f_S\)) de los datos de tiempo, utilizada en el análisis FFT, establece el límite de frecuencia superior en los espectros producidos. Este límite se llama Frecuencia de Nyquist o \(f_N\) y se define como:
Por ejemplo, si los datos adquiridos se muestrean con 20 kHz, entonces el límite de frecuencia superior de los espectros en frecuencia será de 10 kHz.
Frecuencia de muestreo y Ancho de Banda
En muchas soluciones de análisis FFT, el ancho de banda de adquisición (\(BW_{Acq}\)) se denomina intervalo de frecuencia válido/útil disponible para fines de análisis FFT.
El ancho de banda de adquisición a menudo se considera más bajo que la frecuencia de Nyquist. Aunque la frecuencia de Nyquist establece un límite de frecuencia superior en \(f_S / 2\) en los espectros FFT producidos, el ancho de banda de adquisición utilizable suele ser incluso menor. Esto se debe a los efectos del convertidor de analógico a digital (ADC), como los efectos de alisado que no se eliminaron por completo con los filtros antialisamiento (AAF).
Como resultado, el ancho de banda de adquisición a menudo se define por una fracción de 1/2,56 o alrededor del 40 % de la frecuencia de muestreo.
Por ejemplo, si adquirimos una serie de datos en el tiempo con una frecuencia de muestreo de 20 kHz, el ancho de banda de adquisición válido (sin fenómenos de filtrado y aliasing) es de 7,812 kHz, como se muestra aquí:
Ancho de Banda
El análisis de ancho de banda es el intervalo de frecuencia válido/útil que ha sido procesado por el analizador FFT.
El análisis de ancho de banda, también denominado frecuencia máxima (\(f_{Span}\)), puede tener un ancho de banda diferente a \(BW_{Acq}\), pero no mayor que \(BW_{Acq}\).
Por ejemplo, al analizar una señal que solo contiene componentes en frecuencia relevantes en una región de frecuencia más pequeña de \(BW_{Acq}\), then \(f_{Span}\) podría elegirse más estrecho que \(BW_{Acq}\).
A menudo, de forma predeterminada, los analizadores FFT utilizan el mismo ancho de banda de análisis que el ancho de banda de adquisición.
Por ejemplo, considere datos de tiempo con una frecuencia de muestreo de 20 kHz: si el analizador FFT está configurado para analizar la señal muestreada completa, producirá espectros con líneas desde CC y hasta \(f_N\)=10 kHz,pero solo las líneas hacia arriba a \(f_{Span}\) = 7.812 kHz estará libre de alisamiento.
Muchas soluciones de analizador FFT solo muestran las frecuencias hasta \(f_{Span}\), aunque pueden almacenar contenido de frecuencia hasta \(f_N\).
Resolución en Frecuencia VS Espacio Entre Líneas
Los términos "Resolución de frecuencia" \(\Delta f_{NBW}\)(también conocido como ancho de banda de resolución \(Res_{BW}\), o simplemente ancho de banda \(B\)) y "Espaciado de línea" a menudo se intercambian, pero hay distinciones entre los dos.
Mientras que el término Espaciado de línea \(f_N\) and \(N\), the term Frequency Resolution \(\Delta f_{NBW}\) takes the Noise Bandwidth (NBW) of the time weighting window into account. See more about window functions in the section Time weighting windows.
Las ventanas de ponderación de tiempo se utilizan de forma predeterminada en el análisis FFT para reducir la fuga espectral. Estas ventanas de ponderación difunden energía adicional de los componentes de frecuencia a las líneas espectrales vecinas. Básicamente, la energía adicional distribuida por la función de ventana está relacionada con el NBW de la función de ventana. Debido a \(NBW\) la resolución de frecuencia real empeora (\(\Delta f_{NBW}\) es mayor) que el espaciado de línea \(\Delta f\):
Diferentes tipos de ventanas tienen diferentes valores de \(NBW\) vguales o mayores que 1.
Como resultado, la resolución en frecuencia real suele ser peor que el espacio entre líneas (consulte la referencia 4.1).
Escala de Amplitud
La escala de amplitud determina cómo se escalan las amplitudes de las líneas espectrales de FFT.
Según el tipo de señal específico y el tipo de medición realizada, ciertas funciones de escalado serán más convenientes y se utilizarán mejor.
Normalmente, varias funciones de escala están disponibles en la configuración del analizador FFT o en la configuración de visualización espectral.
Además de las funciones de escala, hay diferentes formatos de escala (o formatos de "lectura") para elegir. Las funciones y formatos de escalado se describen a continuación.
Funciones de Escalamiento
Cuando se configuran los analizadores FFT, en algún momento el usuario debe determinar cómo se debe escalar la amplitud de los datos espectrales cuando se almacenan o muestran. Las funciones de escala más comunes son:
Lineal
Potencia
PSD (densidad espectral de potencia)
ESD (densidad espectral de energía)
ASD (densidad espectral de amplitud)
Escala Lineal
El escalado lineal genera la misma unidad que la unidad de señal de entrada:
El escalado lineal normalmente se elige para señales periódicas deterministas estacionarias, por ejemplo, para analizar los armónicos sinusoidales de la maquinaria rotatoria.
Con el escalado lineal, las señales sinusoidales periódicas se pueden superponer y comparar independientemente del espaciado entre líneas seleccionado, ya que la energía de los componentes sinusoidales individuales permanecerá (más o menos) en una línea espectral.
Escalado de Potencia
El escalado de potencia genera el cuadrado de la unidad de señal de entrada:
El escalado de potencia se elige por las mismas razones que el escalado lineal. Pero mientras que el escalado lineal es proporcional a la unidad de entrada, el escalado de potencia es proporcional a la potencia de la unidad de entrada. Esto tiene algunas ventajas cuando se inspeccionan los datos espectrales o cuando se usan los datos espectrales para crear canales matemáticos derivados.
Escalado PSD
El escalado de densidad espectral de potencia (PSD) genera la potencia dividida por \(\Delta f_{NBW}\):
El escalado de PSD se puede interpretar como la potencia en frecuencia y normalmente se elige para señales aleatorias de banda ancha estacionarias, por ejemplo, para cuantificar la fatiga por vibración aleatoria.
Con el escalado PSD, los datos aleatorios de banda ancha pueden superponerse y compararse independientemente del Espaciado entre líneas seleccionado en el analizador FFT, ya que tiene en cuenta la Resolución de frecuencia (consulte la referencia 2.1).
Escalamiento ESD
El escalado de densidad espectral de energía (ESD) genera la PSD integrada durante el tiempo promedio espectral:
El escalado ESD se puede interpretar como la energía en frecuencia y normalmente se elige para señales transitorias no estacionarias con energía finita en el tiempo, por ejemplo, al realizar mediciones de impacto.
Escalamiento ASD
El escalado de Densidad espectral de amplitud (ASD) o Densidad espectral lineal (LSD) genera la raíz cuadrada de PSD:
El escalado ASD se usa a veces para datos aleatorios de banda ancha que tienen una forma de espectro bastante constante, ya que las variaciones en ASD serán proporcionales a las variaciones en el nivel de la señal de entrada.
Formatos de escala
Después de seleccionar la función de escalado más adecuada para un escenario de medición determinado, los analizadores FFT suelen proporcionar un conjunto de formatos de escalado que especifica cómo deben interpretarse los datos espectrales.
Normalmente, las relaciones entre los formatos de escala en los analizadores FFT se basan en la suposición de que las líneas espectrales representan sinusoides individuales. Por lo tanto, se cumplen las siguientes relaciones:
El pico (pk) es la amplitud del pico positivo de la señal
RMS (rms - Root Mean Square) es la amplitud de la señal rms. Para sinusoides, rms se relaciona con el valor pico por:
Pico a pico (pkpk) es la amplitud de pico mínima a máxima de la señal. Para sinusoides, pkpk se relaciona con el valor pico por:
Promedio (avg) es la media de todos los valores absolutos de la forma de onda. Para sinusoides, avg se relaciona con el valor máximo por:
A partir de estas relaciones de escala de amplitud, también se pueden determinar el factor de cresta y PAPR.
El factor de cresta C (también conocido como factor de pico kp o factor de amplitud) es la relación entre el pico y la amplitud rms, que indica la fuerza de los picos en la forma de onda en comparación con el valor rms efectivo. Un factor de cresta de 1 indica que no hay picos, mientras que, por ejemplo, una onda sinusoidal típica tiene un factor de cresta de \(\sqrt{2} \simeq 1.414\) (consulte la referencia 5.2).
Además, mediante el uso de la función de escalado de potencia, se puede determinar la relación de potencia máxima a media (PAPR). Se define por la relación de potencia entre el pico y la amplitud rms, e indica la potencia de los componentes pico en las señales en comparación con la amplitud cuadrática media.
PAPR normalmente se expresa en decibelios:
Ventanas de Ponderación de Tiempo
En resumen, los analizadores FFT utilizan funciones de ventana de ponderación temporal para reducir la fuga espectral. Tal fenómeno de fuga provoca errores de amplitud en el espectro en frecuencia.
Corrimiento de Frecuencias
La desviación espectral ocurre cuando la energía de los componentes en frecuencia en una señal se distribuye en una amplia gama de líneas espectrales en lugar de estar representada por líneas espectrales individuales.
Básicamente, la fuga de energía espectral surge cuando las señales analizadas contienen energía en frecuencias no descritas por las líneas espectrales del espectro FFT.
Por ejemplo, configurar un analizador FFT con un espacio entre líneas de 2 Hz; si la señal analizada contiene energía a una frecuencia irregular como 10,5 Hz, por ejemplo, se producirán fugas. ¿Por qué? porque ninguna línea espectral única puede describir la energía a 10,5 Hz cuando el espacio entre líneas es de 2 Hz.
Este fenómeno de fuga surge porque los algoritmos FFT describen bloques de datos de tiempo con componentes sinusoidales periódicas. Tal representación requiere que las señales de tiempo se periodicen en bloques de tiempo que sean continuos en los extremos donde los bloques se unen efectivamente en un bucle.
Recuerde que la longitud del bloque de tiempo FFT \(T\) está definida por el recíproco del espacio entre líneas:
Dado un espaciado de línea espectral de 2 Hz, la duración del bloque de tiempo es de 0,5 segundos. Esto hace que todos los componentes de frecuencia desiguales tengan discontinuidades en los extremos del bloque en bucle. Agregando al ejemplo de hace dos párrafos, 10,5 Hz tendrá una diferencia de fase de 90 grados entre los extremos del bloque.
Si las señales de tiempo se periodizan para tener una longitud de bloque \(T\) que hace que los bloques de tiempo tengan discontinuidades en los extremos, los algoritmos FFT intentarán representar dichas discontinuidades filtrando una parte de la energía a una amplia gama de componentes sinusoidales.
Para la mayoría de los tipos de señales, es difícil o imposible encontrar longitudes de bloque sin discontinuidades en los extremos del bloque ciclico de tiempo y, por lo tanto, se utilizan funciones de ventana de ponderación de tiempo para ayudar a resolver este problema.
Concepto de Funciones Ventana
Las técnicas de ponderación de tiempo agregan una "ventana" con coeficientes de ponderación individuales a cada muestra de tiempo en un bloque de tiempo de FFT. Esto reduce principalmente aquellas muestras que causan fugas espectrales. En efecto, las muestras en los extremos del bloque de tiempo se reducen a cero (o muy reducidas), de modo que se eliminan las discontinuidades en la señal de tiempo periodica.
En la siguiente imagen se ilustran ejemplos de algunas formas de función de ventana:
Los parámetros que caracterizan las funciones de ventana se enumeran a continuación:
NBW
Error de amplitud máxima (también conocido como ondulación)
Selectividad
Ancho de Banda de Ruido Efectivo (NBW)
El Ancho de banda de ruido efectivo, se define como el ancho de un filtro ideal que transmite la misma potencia desde una fuente de ruido blanco que el filtro dado/usado (consulte la referencia 3.1).
El NBW de un filtro indica qué tan bien separa los componentes de frecuencia de amplitudes similares y, por lo tanto, determina la resolución de frecuencia \(\Delta f_{NBW}\).
Dado que el NBW indica el ancho de un filtro ideal que transmite la misma potencia de ruido blanco que el filtro, a la inversa, indica cuánta potencia adicional agrega el filtro al bloque de tiempo.
La cantidad de potencia adicional debe tenerse en cuenta, por ejemplo, al sumar la potencia de un intervalo de líneas espectrales y al usar escalas de amplitud como PSD. Esta es la razón por la que el escalado de PSD usa \(\Delta f_{NBW}\) no solo \(f\).
Otro parámetro de ancho de banda que se menciona a veces es el ancho de banda a 3 dB o \(BW_{3dB}\), pero en la mayoría de los filtros prácticos, la diferencia entre el ancho de banda 3 dB y el NBW es relativamente pequeña (consulte la referencia 3.2).
Rizado (Error de Amplitud Máxima)
La ondulación, también conocida como Planitud o Pérdida festoneada, indica el error de amplitud máximo dentro de \(± \Delta f/2\) alrededor de una línea espectral y, por lo tanto, determina la exactitud de la amplitud de la señal. Este error de amplitud máxima también se conoce como el error de efecto de cerca de piquete máximo.
Selectividad
La selectividad de un filtro determina la capacidad de separar componentes con diferentes niveles y se define por:
Lóbulo lateral más alto
Tasa de caída del lóbulo lateral
Ancho de banda de 60 dB o \(BW_{60dB}\)
Factor de forma
Las funciones de ventana no eliminan por completo el corrimiento de frecuencia y los lóbulos laterales seguirán existiendo, pero están más atenuados. Los parámetros de selectividad que describen tales características de lóbulo lateral se ilustran en la siguiente imagen:
Cuando las señales tienen componentes de frecuencia de niveles muy diferentes, la función de ventana debe tener una buena selectividad para separarlos. La buena selectividad se logra principalmente al tener un factor de forma pequeño, lo que indica faldas de filtro empinadas. Pero el ancho de banda de 60 dB debe ser relativamente estrecho si dos componentes tan diferentes están muy próximos entre sí.
Tipos de Ventana
La elección de qué función de ventana usar depende del contenido en frecuencia de la señal. Algunas funciones de ventana tienen un ancho de banda de ruido relativamente pequeño que proporciona una buena resolución en frecuencia \(f_{NBW}\), como la ventana de Hanning.
Se desea una buena resolución de frecuencia para las señales que contienen componentes de interés de frecuencia estrechamente espaciados con niveles de amplitud similares.
Otras funciones de ventana tienen mayor \(NBW\) como la ventana Flattop, sin embargo, Flattop funciona mejor en la determinación de los niveles de amplitud exactos debido a su bajo valor de ondulación.
Si es necesario separar dos tonos estrechamente espaciados con niveles de amplitud muy diferentes, entonces se deben usar funciones de ventana con buena selectividad. Por ejemplo, si tiene un ancho de banda estrecho de 60 dB y un valor pequeño para el lóbulo lateral más alto, es más probable que el componente tonal débil sea detectable a partir de la dispersión de energía del componente tonal fuerte.
Las ilustraciones a continuación muestran simulaciones de algunas funciones de ventana comunes y sus diferencias con respecto al NBW, la ondulación y la selectividad.
A partir de las simulaciones de funciones de ventana ilustradas anteriormente, se pueden determinar los parámetros característicos de las funciones de ventana. Consulte la tabla a continuación:
| Window function | NBW | Ripple | \(BW_{3dB}\) | \(BW_{60dB}\) | Shape factor | Highest sidelobe | Sidelobe fall-off rate per decade |
|---|---|---|---|---|---|---|---|
| Rectangular | 1.00 \(\Delta f\) | -3.92 dB | 0.89 \(\Delta f\) | 665 \(\Delta f\) | 750 | -13.3 dB | -20 dB |
| Hanning(\(\alpha = 2\)) | 1.50 \(\Delta f\) | -1.42 dB | 1.44 \(\Delta f\) | 13.3 \(\Delta f\) | 9.2 | -31.5 dB | -60 dB |
| Hamming | 1.36 \(\Delta f\) | -1.75 dB | 1.30 \(\Delta f\) | 94.1 \(\Delta f\) | 72.4 | -42.7 dB | -20 dB |
| 5-term Flat top* | 3.77 \(\Delta f\) | -0.01 dB | 3.72 \(\Delta f\) | 9.2 \(\Delta f\) | 2.5 | -93.0 dB | -20 dB |
| Blackman | 1.73 \(\Delta f\) | -1.10 dB | 1.64 \(\Delta f\) | 9.2 \(\Delta f\) | 5.6 | -58.1 dB | -60 dB |
| 7-term Blackman-Harris | 2.63 \(\Delta f\) | -0.48 dB | 2.48 \(\Delta f\) | 10.2 \(\Delta f\) | 4.1 | -180 dB | -20 dB |
Hay muchos tipos de funciones de ventana más allá de las enumeradas en la tabla anterior, algunas de las cuales tienen parámetros definidos por el usuario. Ejemplos de ventanas con parámetros definidos por el usuario son ventanas transitorias formadas como ventanas rectangulares, pero solo dentro de la duración definida por el usuario del bloque FFT. Fuera de esa duración transitoria, la ventana de tiempo transitorio tiene valores cero. En la mayoría de las implementaciones de ventanas transitorias, el usuario también puede especificar la disminución de los bordes de ataque y de salida para evitar cortar el ruido de fondo demasiado bruscamente, lo que puede provocar fugas.
Otro tipo de ventana con parámetros de entrada es la ventana exponencial con la constante de decaimiento como parámetro definido por el usuario. El usuario puede ajustar la ventana para que se ajuste al decaimiento de "timbre" de las respuestas estructurales después de una excitación de entrada transitoria, o ajustar la ventana para que decaiga con un cierto nivel durante la duración del bloque de tiempo de FFT, entre otras variaciones.
¿Qué función de ventana usar?
La función de ventana óptima para usar depende de las señales que necesita analizar.
Ventanas para señales transitorias
Cuando se analizan señales transitorias, la ventana Rectangular debe usarse por defecto. Pero la ventana de transitorios debe usarse para transitorios que son relativamente cortos en comparación con la longitud del bloque FFT, para filtrar el ruido no relacionado y mejorar la relación señal-ruido.
Se deben usar ventanas exponenciales si la duración de los transitorios excede la longitud del bloque FFT. En estos casos, el uso de ventanas exponenciales puede garantizar que el transitorio decaiga lo suficiente dentro de la longitud del bloque FFT, lo que reduce las fugas.
Si los transitorios son relativamente largos en comparación con el bloque de tiempo de FFT, entonces se puede usar la ponderación de Hanning junto con una superposición de bloque de tiempo de FFT de ⅔ o ¾ (consulte la referencia 3.2).
Ventanas para Señales Continuas
Una opción popular es la ventana de Hanning. Esta ventana tiene un lóbulo principal bastante estrecho, por lo tanto, una buena resolución de frecuencia y una supresión razonable del lóbulo lateral, lo que la hace adecuada para muchas aplicaciones.
La ventana de Blackman tiene un mejor rechazo y selectividad del lóbulo lateral en comparación con Hanning, pero el lóbulo principal es un poco más ancho. En muchos casos, se selecciona un número suficiente de líneas FFT para tener componentes de frecuencia relevantes separados con múltiples líneas espectrales. El lóbulo principal más ancho de Blackman es una buena compensación para lograr menos fugas en los contenedores vecinos.
La ventana Blackman-Harris de 7 términos tiene un excelente rechazo de la banda lateral, pero un lóbulo principal relativamente ancho. Esto se puede usar para analizar señales que tienen componentes en frecuencia con niveles de amplitud muy diferentes.
Si la precisión de la amplitud es la máxima prioridad, se debe utilizar la ventana Flat-top. Esto permite una imprecisión de amplitud de solo 0,01 dB. La compensación es que el NBW grande causa una resolución en frecuencia menos buena. Esta ventana es la más adecuada para la calibración.
Para señales continuas, la ventana rectangular solo debe usarse para analizar señales sinusoidales específicas que contengan solo componentes en frecuencia que se alineen con las líneas espectrales de FFT, y no entre ellas. Si se cumplen estas condiciones, el tipo de ventana rectangular funcionará muy bien con fugas mínimas. Pero si existen componentes sinusoidales entre las líneas espectrales, la ventana rectangular provocará una gran fuga.
Las señales que contienen solo componentes sinusoidales en las líneas espectrales suelen ser la situación en las aplicaciones de análisis de orden. El análisis de orden vuelve a muestrear los datos de tiempo con respecto a la velocidad de rotación. Otro caso es cuando se utilizan señales pseudoaleatorias. Para obtener más información sobre señales pseudoaleatorias, consulte la referencia 1.3.
Ventanas para Señales Aleatorias
Para señales aleatorias continuas normales, a menudo se prefiere la ventana de Hanning para reducir las fugas debido a su buena resolución en frecuencia. Se pueden elegir señales aleatorias para pruebas de vibración y pruebas de dinámica estructural, por ejemplo, donde un vibrador vibratorio o vibrador modal utiliza estos tipos de señales para excitar la estructura.
Para señales aleatorias pseudoaleatorias y periódicas, se debe usar la ventana rectangular porque proporciona mediciones sin fugas.
Las señales de impacto y las señales aleatorias de ráfaga deben analizarse como se describe para las señales transitorias. Es típico usar una ventana transitoria para transitorios cortos y una ventana exponencial para transitorios más largos. Por ejemplo, al realizar un análisis estructural usando un martillo de impacto para proporcionar una señal de excitación y un acelerómetro para capturar la respuesta, la señal de excitación corta debe usar una ventana transitoria mientras que la señal de respuesta más larga debe usar una ventana exponencial.
Promedio
El promedio se puede realizar en el dominio del tiempo o en el dominio de la frecuencia. En esta sección, nos centraremos principalmente en promediar en el dominio de la frecuencia, que es el principal tipo de promediación que se usa con los analizadores FFT. El promedio en el dominio de la frecuencia a veces se denomina promedio de espectro.
Los analizadores FFT a menudo tienen diferentes opciones para configurar el proceso de promedio de espectro. Los modos de promedio más comunes se describen en las siguientes secciones.
Promedio RMS
El promedio de RMS (también conocido como promedio de espectro de potencia o promedio de energía) suele ser el modo de promedio de espectro predeterminado en los analizadores FFT.
El promedio RMS se utiliza para reducir la fluctuación de los niveles de ruido espectral. Con el promedio de espectro RMS, las líneas espectrales individuales se promedian sobre múltiples espectros de potencia instantánea o espectros de potencia cruzada.
En la siguiente imagen, un espectro de potencia instantánea no promediado (rojo) se compara con un espectro promediado sobre 100 espectros de potencia (azul).
Al realizar un promedio de RMS, el ruido en la señal se promedia de la misma manera que la señal pura/consistente. Como resultado, el ruido no se reduce ni se promedia mediante la promediación del espectro, pero los niveles de ruido espectral serán cada vez más estables (promediados) con un número creciente de espectros promediados.
La desviación estándar del ruido aleatorio en los espectros promediados RMS se reducirá por un factor de \(1/ \sqrt{N}\), donde\(N\) es el número de espectros instantáneos promediados (consulte la referencia 6.1). Esta es una reducción de la desviación estándar de -5 dB cada vez que el número de promedios es 10 veces mayor. Por el contrario, el tiempo de medición aumentará a medida que aumente el número de promedios.
El promedio RMS calcula la suma de potencia media que se relaciona con la energía media. La raíz cuadrada de la suma de la potencia media se calcula para generar la misma unidad que la señal de entrada: raíz cuadrada media. En cuanto a todos los modos de promedio de espectro, el promedio se realiza para todas las líneas espectrales individualmente.
Promedio de Espectro Complejo
Algunos analizadores FFT admiten el promedio de espectro complejo. Este método calcula la media sobre los espectros FFT instantáneos complejos, para todas las líneas espectrales. El promedio de espectro complejo se puede utilizar para reducir los niveles de ruido y otros componentes inconsistentes en los espectros. Su rendimiento es similar al promedio síncrono en el dominio del tiempo.
Al realizar el promedio de espectros complejos instantáneos, se promediarán los componentes de amplitud con características de fase variables en los espectros. El ruido aleatorio se puede reducir, pero la señal relevante también se puede reducir si el analizador FFT no está configurado correctamente. Esto debe evitarse.
Si los componentes de la señal relevantes tienen características de fase variables, como los componentes de ruido, entonces el espectro resultante también obtendrá el promedio de esos componentes relevantes.
Para evitar la reducción de los componentes de señal relevantes, se puede utilizar un disparador de bloque FFT. De esta forma, las características de fase de los componentes de señal relevantes pueden mantenerse de manera que solo se reduzca el ruido.
Otra forma de hacer que el promedio de espectro FFT complejo funcione como se desea en las pruebas estructurales multicanal es definir un canal de referencia y medir su espectro de referencia de fase instantánea. Agregar los mismos cambios de fase a todos los espectros de canal según sea necesario para que el espectro de referencia de fase mantenga una fase constante a lo largo del tiempo (para todos los componentes espectrales), hará que los componentes de frecuencia relevantes sean consistentes para todos los canales. De esta manera, el promedio complejo solo promediará los componentes de ruido (consulte la referencia 2.2).
Utilizando el promedio de espectro complejo, los componentes de ruido aleatorio inconsistentes en el espectro promediado se pueden reducir en 1/N, donde N es el número de espectros FFT instantáneos complejos promediados. Esto es -10 dB cada vez que el número de promedios es 10 veces mayor (ver referencia 3.3).
Promedio Espectral Lineal o Exponencial
Cuando el promedio se realiza con pesos iguales para todos los espectros instantáneos, se denomina promedio lineal. Por ejemplo, el promedio RMS lineal general se realiza cuando el contenido de energía es igualmente importante durante todo el tiempo de medición.
El promedio lineal a menudo se puede configurar para cubrir una cierta duración de tiempo, o una cantidad de espectros FFT, donde todos los datos tienen la misma ponderación. Por ejemplo, en un escenario de usuario, podría desearse promediar la energía de vibración o determinar los niveles de presión de sonido espectral equivalente durante un cierto período de tiempo.
Si los espectros instantáneos más nuevos deben ponderarse más que los espectros más antiguos que están involucrados en el proceso de promedio, entonces se puede usar el promedio exponencial en lugar del promedio lineal.
Con el promedio exponencial, la influencia de los espectros decae exponencialmente con el tiempo. Normalmente, el operador del analizador FFT puede ajustar un parámetro relacionado con la constante tau de disminución del tiempo exponencial. De esta forma se establece la ponderación de los diferentes espectros involucrados.
El promedio exponencial se usa especialmente para monitorear señales no estacionarias con niveles de amplitud variables. Dado que el espectro más nuevo tiene una ponderación mayor que los espectros anteriores, los eventos repentinos se indicarán con más fuerza en el espectro promediado cuando se usa un promedio exponencial que cuando se usa un promedio lineal.
Retención Máxima
Aunque la retención máxima no realiza el promedio, a veces se incluye en los modos de promedio disponibles para los analizadores FFT. Esto podría deberse al hecho de que en el proceso intervienen múltiples espectros instantáneos, como cuando se realiza un promedio.
La retención máxima mantiene el valor máximo de las líneas espectrales individuales durante el tiempo promedio especificado. Como resultado, el espectro de retención máximo resultante podría tener algunas líneas espectrales que contienen valores de algunos espectros instantáneos y otras líneas que contienen valores de otros espectros instantáneos.
La retención espectral máxima se puede utilizar para la inspección de los peores escenarios, al obtener un espectro que indique las amplitudes máximas para todas las frecuencias durante un tiempo de prueba determinado.
Superposición
Dentro del contexto del análisis FFT, el parámetro Superposición se refiere a bloques de tiempo FFT superpuestos.
La superposición se puede utilizar para calcular espectros FFT de manera más consistente cuando se aplican funciones de ventana y para aumentar la tasa de espectros producidos.
Debido a que los analizadores de FFT producen un espectro para cada bloque de tiempo de FFT, cuando estos bloques se superponen, el análisis producirá espectros con una tasa mayor en comparación con cuando no se utiliza superposición (0 % de superposición). Esto aumenta la tasa de actualización de las pantallas espectrales, pero a la inversa, los espectros incluirán contenido de señal superpuesto.
Los bloques FFT con ponderación de ventana suelen tener valores muy pequeños (o cero) cerca de los límites del bloque, como se muestra en la figura anterior. Los valores reducidos cerca de los límites afectan a una parte significativa de la señal de tiempo que se ignora de forma efectiva en el proceso de análisis. En situaciones de medición donde los datos se recopilan a un gran costo, esta situación debe evitarse. Se pueden usar bloques de FFT superpuestos para mejorar esto (consulte la referencia 6.1).
Al usar ventanas rectangulares, todos los valores de los bloques ya tendrán la misma ponderación, y la superposición solo ayudará a aumentar la tasa de espectros producidos.
Los bloques de FFT superpuestos se pueden ajustar para obtener la misma ponderación para todas las muestras de tiempo en múltiples espectros superpuestos, dando una representación de frecuencia de una señal de tiempo plana (igualmente ponderada). Esto se usa para obtener resultados equivalentes a un análisis en tiempo real, donde la función de ponderación general debe ser uniforme, por ejemplo, cuando se usa la ponderación de Hanning. La superposición debe ser de al menos ⅔ para obtener esto (ver referencia 3.2).
A medida que aumenta la superposición, los espectros FFT también se correlacionarán cada vez más con los espectros posteriores. En muchos casos, los espectros correlacionados son innecesarios y, por lo tanto, no se gana mucho después de alcanzar una fracción de superposición que proporciona pesos generales casi iguales para las muestras de tiempo. Por lo tanto, la fracción de superposición ideal a menudo se determina para equilibrar pesos totales iguales de muestras y correlación pequeña.
Aunque la superposición ideal depende de la función de la ventana y el tipo de señal medida, una fracción de superposición razonable para usar suele ser ⅔ o ¾.
Funciones Adicionales Utilizadas con el Análisis FFT
Para aprovechar al máximo el análisis FFT, a menudo se utilizan características adicionales para mejorar el análisis y el diagnóstico. Esta sección mencionará algunas de las características comunes que pueden admitir los analizadores FFT.
Curvas de Referencia, Tolerancias y Detección de Alarmas
Las curvas de referencia, que indican cómo debería verse idealmente el contenido espectral de las señales, se pueden usar en el monitoreo de señales para detectar cambios críticos en la evolución de la señal.
Por ejemplo, al monitorear maquinaria en funcionamiento, se capturó una curva de referencia ideal inicial. A partir de ese momento, los nuevos datos de la máquina se pueden superponer visualmente y comparar con el espectro de referencia. Con esta técnica, se pueden detectar defectos en evolución y se puede programar el mantenimiento.
Las curvas de tolerancia espectral también se pueden utilizar para establecer un límite de tolerancia inferior y/o superior para lo que se define como niveles espectrales aceptables.
Otro ejemplo del uso de curvas de tolerancia es cuando se monitorean los niveles de ruido espectral. Se pueden evaluar niveles de tonos perturbadores específicos que podrían no ser detectados por el nivel de presión de sonido total (SPL). Incluso los entornos con ruido agradable pueden tener componentes tonales que causen incomodidad.
Es posible que el SPL total no indique tonos desagradables debido a todo el ruido de banda ancha, pero al observar el contenido espectral, dichos tonos se indicarán con niveles más altos en comparación con el ruido de banda ancha. Para monitorear y regular el ruido percibido, se pueden establecer límites de tolerancia espectral de acuerdo a lo que se define como niveles aceptables.
Para aplicaciones críticas y campañas de prueba, es posible que se requiera detección de alarmas para garantizar acciones correctivas rápidas. Esto es especialmente cierto en los casos en que se exceden los niveles de tolerancia. Por ejemplo, al realizar pruebas estructurales críticas, se pueden definir los niveles máximos de deflexión aceptados que no deben superarse durante la prueba. En estos casos, la funcionalidad de detección de alarma se puede utilizar para detener automáticamente la prueba si se alcanzan niveles inaceptables o inseguros.
Cálculos Escalares
Durante el análisis FFT, puede ser beneficioso extraer el contenido de energía de rangos/secciones de frecuencia fijos de interés. Esto también se conoce como un tipo de filtrado en el dominio de la frecuencia.
Algunos analizadores FFT admiten la capacidad de producir canales escalares derivados que generan un valor por espectro producido. Los valores escalares pueden expresar el RMS total o el valor máximo de los rangos de frecuencia definidos por el usuario.
Filtrar energía a excepción de los componentes incluidos en los rangos de frecuencia definidos puede simplificar las tareas de monitoreo y diagnóstico. A veces también mejora la inspección automatizada.
Por ejemplo, si una máquina estacionaria solo necesita una inspección en unas pocas bandas de frecuencia estrechas, los cálculos escalares pueden extraer valores relacionados con esas bandas.
A medida que se extraen y observan más y más características específicas de la señal, mejor se vuelve la visión general del contenido relevante en las señales de tiempo medidas. Esto facilita la configuración de reglas para el monitoreo automatizado.
Los analizadores FFT a menudo admiten muchos cálculos escalares predefinidos y definidos por el usuario que se pueden usar para inspeccionar cosas como componentes de cojinetes cinéticos, relaciones de amortiguamiento estructural SDOF, componentes de señales armónicas y distorsión armónica total (THD).
Estos cálculos brindan información adicional sobre las mediciones y mejoran el proceso de análisis de la señal.
A continuación se muestra otro ejemplo de cálculos escalares de algunos componentes armónicos encontrados al analizar el espectro. Los armónicos pueden indicar distorsión y comportamientos no lineales.
Análisis de Doble Canal
El análisis de doble canal permite analizar una señal en relación con otra señal, a veces denominada señal de referencia. Al analizar la relación entre dos señales, es posible determinar la correlación entre los componentes de magnitud espectral y las diferencias de fase.
Ser capaz de analizar canales en relación con otros canales abre un nuevo conjunto de nuevas funciones que se pueden utilizar en varios dominios. Las funciones de coherencia y respuesta de frecuencia son posibles, pero los tipos de funciones básicas que se utilizan para los cálculos de doble canal son los espectros de potencia y los espectros de potencia cruzada, como se describe en la sección Resultados de los analizadores FFT.
Resultados de Doble Canal
El análisis de doble canal y la capacidad de comparar señales en relación con las señales de referencia hacen posible calcular un grupo de funciones de canales cruzados. Aquí hay una lista de algunos tipos de funciones de canales cruzados bien conocidos:
Espectro cruzado
Correlación cruzada
Función de respuesta de frecuencia (FRF)
ODS FRF
Coherencia (COH)
Potencia de salida coherente (COP)
Densidad espectral de potencia cruzada (CPSD)
Por ejemplo, la función de coherencia expresa la relación lineal entre dos señales en función de la frecuencia. Esto se usa a menudo para verificar la validez de los datos medidos, indicando la influencia del ruido y las no linealidades. La función de coherencia se calcula utilizando los espectros de potencia \(G_{AA}(f)\) y \(G_{BB}(f)\) de las dos señales junto con el espectro de potencia cruzada \(G_{AB}(f)\):
Otro ejemplo de tipos de funciones de doble canal de uso común es la función de respuesta de frecuencia (FRF). Los análisis FRF representan la relación entre la señal de salida\(b(t)\) y la señal de entrada \(a(t)\) de sistemas lineales invariantes en el tiempo, en el dominio de la frecuencia. Se han definido muchas variantes de la función FRF para tener en cuenta efectos como el ruido en las mediciones. Una de las variantes más utilizadas es el FRF \(H_1\) que minimiza los errores relacionados con el ruido en la señal de salida \(b(t)\). FRF \(H_1\) está definido por:
Las funciones FRF se utilizan en las pruebas y análisis modales para estimar las propiedades dinámicas estructurales, como las relaciones de amortiguamiento.
A veces es beneficioso tener un espectro de potencia de una señal \(b(t)\), pero que incluya información de fase, relativa a una señal de referencia \(a(t)\), creando espectros de potencia con la magnitud de la señal \(b(t)\), y con la fase de \(b(t)\) relativa a la señal \(a(t)\). Dichos espectros de potencia con referencia de fase o espectros de fase asignada a veces se denominan ODS FRF porque brindan la información de magnitud y fase requerida para comprender las amplitudes y formas de deflexión en múltiples ubicaciones de sensores de estructuras operativas medidas.
Para un espectro ODS FRF, la magnitud es igual al espectro de potencia \(G_{BB}(f)\), y la fase es igual a la fase del espectro de potencia cruzada \(G_{AB}(f)\).
Análisis Disparado
Los analizadores FFT normalmente están configurados de manera predeterminada para funcionar continuamente. Esto también se conoce como modo libre o modo de ejecución libre. En el modo Libre, el analizador FFT produce espectros continuamente desde el principio hasta el final de la señal de tiempo.
Pero los analizadores FFT también pueden admitir el análisis activado, donde el procesamiento FFT solo se ejecuta cuando se activa para hacerlo.
Si el analizador FFT está configurado para análisis activado, el analizador está en modo de espera hasta que se cumpla la condición de activación. El tiempo de activación definirá la hora de inicio de los bloques de tiempo de FFT y se producirá un espectro en la longitud del bloque de tiempo \(T\) después del tiempo de activación.
El disparador a menudo se puede configurar de varias maneras. Por ejemplo, puede configurarse para que se dispare cuando una señal alcance cierto nivel, o por una acción manual, o por algún evento externo.
El análisis FFT disparado es útil en los casos en que el espectro debe incluir contenido específico relacionado con una acción. Por ejemplo, al realizar pruebas de impacto de martillo, el espectro FFT debe contener la energía relacionada con uno o varios impactos completos. A menos que se utilice un análisis desencadenado, el bloque de tiempo de FFT tendrá una hora de inicio en una posición de tiempo aleatoria y es posible que solo incluya una fracción del evento de impacto.
En otros casos, los estándares pueden requerir que los espectros FFT se hayan activado en relación con algún parámetro externo, como la velocidad, la posición o la potencia. Por ejemplo, al realizar pruebas de ruido de paso de automóviles, es posible que los espectros deban ser activados por ciertas posiciones del automóvil en relación con la pista de prueba, para garantizar la reproducibilidad de las mediciones.
Filtración
Una característica utilizada en varios dominios para mejorar la inspección de los espectros FFT es el filtrado de señales. El filtrado se puede realizar para reducir el ruido, atenuar ciertos componentes de frecuencia o caracterizar los componentes de frecuencia con coeficientes de ponderación individuales, para tener en cuenta otros parámetros.
El grado de compatibilidad de los analizadores FFT con diferentes tipos de filtros varía. La mayoría de los analizadores admiten filtros básicos como la ponderación acústica, pero algunos analizadores FFT también admiten otros tipos de filtros predefinidos y filtros derivados del usuario.
Según el tipo de filtro y el analizador de FFT utilizado, algunos filtros procesan las señales de tiempo antes del cálculo de FFT, mientras que otros filtran los espectros de FFT después. Es posible que los filtros deban configurarse en módulos de procesamiento de filtros separados, pero algunos analizadores FFT admiten directamente la configuración de muchos filtros de uso común.
Ponderación Acústica
Cuando se analizan señales de sonido y ruido, se pueden aplicar filtros de ponderación acústica para tener en cuenta la percepción humana audible. Los humanos no perciben que todos los componentes de frecuencia sean igualmente fuertes, aunque tengan el mismo nivel de presión de sonido. Los filtros acústicos se definen para tener en cuenta esa percepción del sonido.
La ponderación A se aplica a los niveles de sonido medidos por instrumentos en un esfuerzo por tener en cuenta el volumen relativo percibido por el oído humano, ya que el oído es menos sensible a las frecuencias de audio más bajas (consulte la referencia 5.1).
La ponderación B se usa para niveles intermedios y es similar a la A, excepto por el hecho de que la atenuación de baja frecuencia es mucho menos extrema aunque significativa (-10 dB a 60 Hz). Esta es la mejor ponderación para usar con fines de escucha musical.
La ponderación C es similar a A y B en lo que respecta a las frecuencias altas. En el rango de baja frecuencia, proporciona poca atenuación. Esta ponderación se utiliza para ruido de alto nivel.
La ponderación D se diseñó específicamente para medir el ruido de aeronaves de alto nivel. El gran pico en la curva de ponderación D no es una característica de los contornos de igual volumen, sino que refleja el hecho de que los humanos escuchan el ruido aleatorio de manera diferente a los tonos puros, un efecto que es particularmente pronunciado alrededor de los 6 kHz (consulte la referencia 1.1).
Tenga en cuenta que, dado que el procesamiento auditivo humano en la cóclea del oído interno se puede comparar con un grupo de filtros de banda de ⅓ de octava, los analizadores de octava a menudo se usan junto con la ponderación acústica para analizar señales que tienen múltiples tonos en una banda de ⅓ de octava o que tienen banda ancha. ruido, con el fin de calcular los niveles de presión acústica ponderados acústicamente de banda de ⅓ de octava percibidos.
Los niveles de presión de sonido ponderados acústicamente generalmente indican el tipo de ponderación en la unidad, p. dBA, o dB(A), para SPL ponderado A.
Integración y Diferenciación
Algunos analizadores FFT proporcionan filtros de integración y diferenciación que se pueden usar para transformar una señal de tiempo o un espectro FFT en otro dominio. Un escenario típico para esto es cuando se transforman datos del dominio de aceleración al dominio de desplazamiento. Cambiar la cantidad física al desplazamiento de la aceleración puede ser útil cuando se usan sensores de aceleración y desea inspeccionar los valores de desplazamiento de los espectros FFT.
Por ejemplo, al medir la aceleración sísmica, también podría ser útil ver las amplitudes de desplazamiento en las ubicaciones de los sensores.
Además, al medir máquinas operativas con acelerómetros, la transformación de los datos en desplazamiento permite inspeccionar las amplitudes de deflexión en las posiciones del sensor. Los acelerómetros piezoeléctricos se eligen normalmente para la medición de vibraciones debido a su amplio rango de frecuencia de funcionamiento.
Aunque la integración/diferenciación se puede usar para transformar varias cantidades físicas, como potencia en energía, se usa comúnmente para transformar señales de aceleración, velocidad y desplazamiento en relación con el análisis FFT. A continuación se muestra una tabla que indica el proceso de integración/diferenciación requerido para transformar entre dichas cantidades.
Referencias
Dewesoft
Siemens
What is a Power Spectral Density (PSD)?
Spectrum versus Autopower
Brüel & Kjær
Application Note: Time Windows, by S. Gade, N. Thrane, H. Konstantin-Hansen & J. Wismer
Technical Review: No. 3, 1987, Windows to FFT Analysis (Part 1), by Svend Gade and Henrik Herlufsen
Application Note: Time Domain Averaging Combined with Order Tracking, by N. Johan Wismer
Books
Frequency Analysis - Brüel & Kjær, by R. B. Randall, B. Tech., B.A., 3rd edition from 1987.
Window functions and their applications in signal processing, by K. M. M. Prabhu, 2014
Digital Signal Processing for Measurement Systems, by G. D’Antona and A. Ferrero, 2006, pp. 70–72.
Wikipedia
A-weighting
Crest Factor
Discrete Fourier transform
Otros Artículos
Spectrum and spectral density estimation by the Discrete Fourier transform (DFT), including a comprehensive list of window functions and some new flat-top windows, by G. Heinzel, A. Rudiger, and R. Schilling, Max-Planck-Institut für Gravitationsphysik (Albert-Einstein-Institut), Teilinstitut Hannover.
National Instruments
Application Note 041, The Fundamentals of FFT-Based Signal Analysis and Measurement, by Michael Cerna and Audrey F. Harvey.