domingo, 13 de abril de 2025 · 0 min read
Comprensión de los módulos de Young, de corte y volumétrico además del coeficiente de Poisson en ingeniería
Seguramente has oído hablar del módulo de Young, el módulo de corte, el módulo volumétrico y el coeficiente de Poisson, pero ¿qué significan realmente y cómo se relacionan entre sí? ¿Cómo los utilizan los ingenieros y científicos para evaluar la integridad estructural de productos, máquinas y estructuras críticas?
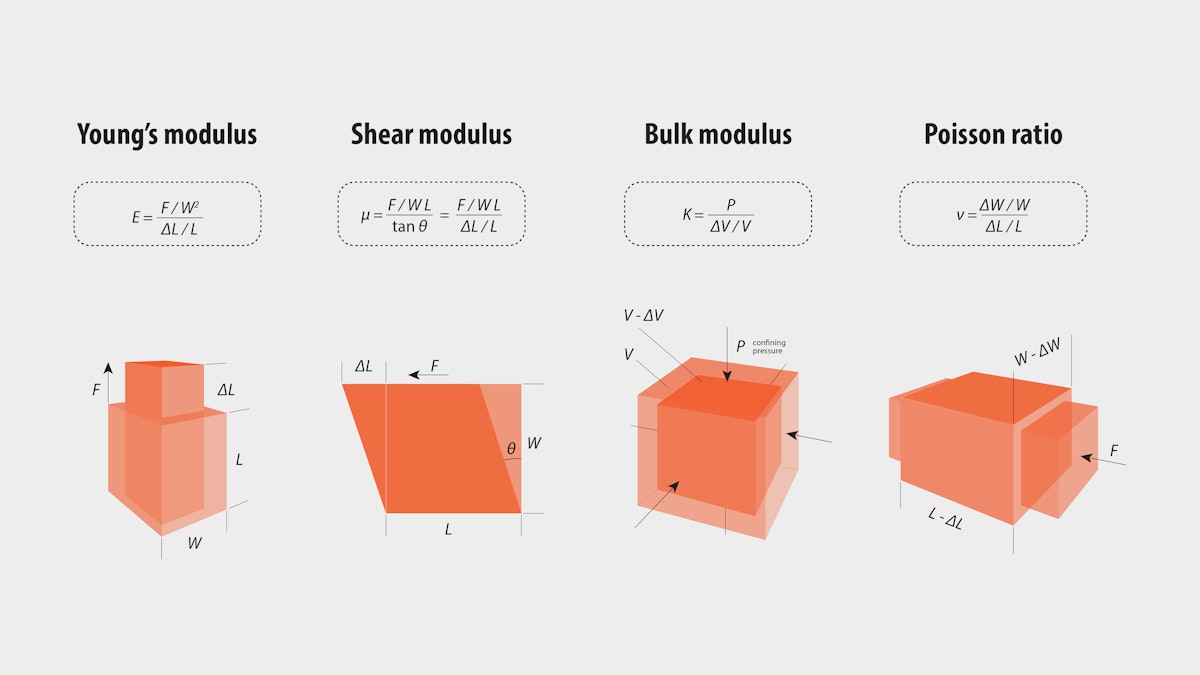
¿Qué son los módulos elásticos?
Un módulo elástico es una propiedad fundamental de un objeto o material que describe su capacidad para deformarse de manera no permanente cuando se le aplica un esfuerzo. Esta propiedad es crucial en la ingeniería, la física y la ciencia de materiales, ya que permite a los ingenieros diseñar estructuras que no se dañen ni colapsen bajo condiciones operativas extremas.
Esfuerzo (σ): Mide la fuerza interna por unidad de área dentro de un material cuando se le aplica una carga externa.
Deformación (ε): Mide el cambio en la forma o longitud del material con respecto a su longitud original.
Módulo de Young (E): Define la rigidez de un material al relacionar el esfuerzo con la deformación dentro de la región elástica (es decir, donde la deformación no es permanente).
Estas propiedades ayudan a los ingenieros a predecir cómo responderán los materiales ante diferentes tipos de cargas, como fuerzas aerodinámicas, diferenciales de presión y esfuerzos estructurales.
El módulo elástico de un objeto o material se puede definir como la pendiente de su curva esfuerzo-deformación. Los materiales más rígidos presentan un módulo elástico más alto en comparación con los materiales menos rígidos.
Donde:
El esfuerzo es la fuerza deformante aplicada dividida entre el área afectada.
La deformación es la relación de cambio, es decir, la cantidad en que cambia la forma de un material en comparación con su estado original.
La deformación es una magnitud adimensional y normalmente se expresa como porcentaje. En el caso del acero, las deformaciones típicas son menores a 2 mm/m y, con frecuencia, se expresan en microdeformaciones (microstrain). Una microdeformación equivale a una deformación de una parte por millón.
Este artículo explica los cuatro principales tipos de módulos elásticos, su importancia, fórmulas, usos en el mundo real y aplicaciones prácticas:
Módulo de Young (E)
Coeficiente de Poisson (ν)
Módulo de corte (G)
Módulo volumétrico (K)
1. Módulo de Young (E)
¿Qué es el módulo de Young?
El módulo de Young, también conocido como módulo de elasticidad, cuantifica la rigidez de un material al medir su capacidad para resistir la deformación axial. Se define como la razón entre el esfuerzo (fuerza por unidad de área) y la deformación (deformación relativa) en una condición de carga uniaxial.
En esencia, el módulo de Young representa la relación entre el esfuerzo y la deformación.
El módulo de Young se mide en unidades del Sistema Internacional: Pascal (Pa o N/m² o kg/m·s²). Los valores típicos se expresan en megapascales (MPa o N/mm²) o gigapascales (GPa o kN/mm²).
En Estados Unidos, comúnmente se expresa en libras por pulgada cuadrada (psi).
Este breve video muestra una prueba típica:
Fórmula del módulo de Young
El módulo de Young se calcula utilizando la siguiente fórmula:
Dónde:
E = Módulo de Young (Pa o N/m²)
σ = Esfuerzo (Fuerza / Área, en Pascales)
ε = Deformación (adimensional, cambio en longitud / longitud original)
Ejemplo del módulo de Young
Los materiales altamente elásticos, como los líquidos y el hule, se deforman fácilmente bajo esfuerzo porque tienen valores bajos de E.
Por el contrario, los metales poseen valores de E muy altos. Al aplicar una carga de compresión o tensión a materiales sólidos, estos sufren una deformación elástica. Este cambio en la forma es reversible cuando se retira la carga. La resistencia inherente de un material determina qué tan grande puede ser la carga antes de que se exceda el límite de deformación elástica y el material ya no pueda recuperar su forma original.
¿La forma de un objeto afecta su módulo de Young?
La forma de los objetos influye considerablemente en su rigidez. Por ejemplo, la forma de una viga en I la hace más resistente a la flexión que una viga recta o una barra del mismo material. Las vigas de acero se diseñan utilizando el módulo de Young para soportar cargas elevadas sin doblarse en exceso. Los rascacielos y los puentes dependen de materiales con un alto módulo de Young para garantizar su estabilidad y durabilidad.
Los sistemas de adquisición de datos (DAQ) de Dewesoft permiten medir en tiempo real el esfuerzo y la deformación. Utilizando amplificadores de galgas extensométricas de alta precisión, los ingenieros pueden registrar con exactitud los datos del módulo de Young durante ensayos de tracción, asegurando que los materiales cumplan con las especificaciones de diseño.
Obtén más información sobre cómo realizar mediciones de deformación que respaldan los cálculos de módulo.
Aplicaciones del módulo de Young
Ingeniería estructural: Determina la capacidad del material para desempeñarse en aplicaciones sometidas a cargas.
Pruebas de materiales: Se utiliza en ensayos de tracción para evaluar el comportamiento mecánico.
Control de calidad: Asegura la uniformidad en la producción de materiales, especialmente en metales, compuestos y polímeros.
Por ejemplo, los fabricantes aeroespaciales utilizan cálculos de esfuerzo, deformación y módulo de Young al diseñar aeronaves y naves espaciales. Estas estructuras están sometidas a cargas de tracción y compresión elevadas en las alas, el fuselaje y los elementos de soporte. También enfrentan cargas vibratorias y cíclicas, particularmente durante el despegue, el vuelo, la reentrada y el aterrizaje. Además, las naves espaciales experimentan fluctuaciones extremas de temperatura.
El módulo de Young ayuda a los ingenieros a seleccionar materiales que no se deformen excesivamente bajo estas condiciones, garantizando la integridad estructural y la seguridad.
2. Coeficiente de Poisson (ν)
¿Qué es el coeficiente de Poisson?
El coeficiente de Poisson describe la relación entre la deformación lateral y la deformación axial en un material sometido a esfuerzo uniaxial. Cuando un material se estira o se comprime, tiende a expandirse o contraerse en dirección perpendicular a la fuerza aplicada.
Por ejemplo, al comprimir una pelota de hule por lados opuestos, se genera una compresión en el eje Y, pero al mismo tiempo se produce una expansión perpendicular en el eje X.
Fórmula del coeficiente de Poisson
Para calcular el coeficiente de Poisson, se utiliza la siguiente fórmula:
Where:
v = (letra griega nu) Coeficiente de Poisson (adimensional)
Ɛlateral = Deformación lateral
Ɛaxial = Deformación axial
Ejemplo del coeficiente de Poisson
Cuando se estira una liga (banda elástica), esta se adelgaza en la parte media debido al efecto del coeficiente de Poisson. Los ingenieros aplican este principio al diseñar materiales flexibles, como empaques de hule y acolchados de espuma.
Los sistemas de adquisición de datos (DAQ) de Dewesoft pueden utilizar medición de deformación multieje para evaluar el coeficiente de Poisson, al capturar simultáneamente los valores de deformación axial y lateral. Esto resulta útil en la validación de materiales para aplicaciones aeroespaciales, automotrices y biomédicas.
Configuración de una galga extensométrica en configuración de cuarto de puente en el software DewesoftX.
Aplicaciones del coeficiente de Poisson
Análisis por elementos finitos (FEA): Permite simular el comportamiento de los materiales sometidos a esfuerzos mecánicos.
Análisis de vibraciones: Es fundamental para predecir la respuesta dinámica de los materiales ante excitaciones mecánicas.
Ingeniería biomédica: Se emplea en la modelación de tejidos biológicos como huesos y tendones.
3. Módulo de corte (G)
¿Qué es el módulo de corte?
El módulo de corte, también conocido como módulo de rigidez, mide la capacidad de un material para resistir deformaciones cuando se le aplica un esfuerzo cortante, es decir, cuando las fuerzas actúan de forma paralela a una de sus superficies, en lugar de perpendicularmente.
Fórmula del módulo de corte
Para calcular el módulo de corte, se utiliza la siguiente fórmula:
Dónde:
G = Módulo de corte (Pa)
𝜏 = Esfuerzo cortante (fuerza por unidad de área)
𝛾 = Deformación cortante (deformación angular en radianes)
Ejemplo del mundo real del módulo de corte
El sistema de suspensión de un automóvil depende de materiales con un módulo de corte específico para absorber las vibraciones del camino y proporcionar una conducción suave. Los bujes de hule en la suspensión ayudan a aislar las vibraciones al resistir la deformación por corte. Cuando se combinan con celdas de carga torsionales, los sistemas de adquisición de datos (DAQ) de Dewesoft permiten medir con precisión el módulo de corte en materiales. Esto es fundamental en pruebas automotrices y sísmicas, donde la resistencia a esfuerzos cortantes determina la seguridad y el rendimiento.
Aplicaciones del módulo de corte
Pruebas torsionales: Determinan la resistencia del material a la torsión.
Industria automotriz: El módulo de corte es clave en las pruebas de suspensión, ya que influye directamente en el comportamiento de los componentes ante esfuerzo y deformación.
Ingeniería sísmica: Permite evaluar cómo responden los materiales y estructuras frente a esfuerzos cortantes durante un sismo.
Análisis de uniones adhesivas: Se utiliza para evaluar el desempeño mecánico de materiales unidos mediante adhesivos.
4. Módulo volumétrico (K)
¿Qué es el módulo volumétrico?
El módulo volumétrico mide la resistencia de un material a la compresión uniforme, cuantificando el cambio de volumen que ocurre al aplicar presión. Mientras que otros módulos como el de Young, el de Poisson y el de corte evalúan esfuerzos aplicados en direcciones específicas, el módulo volumétrico se emplea cuando la compresión proviene de múltiples direcciones al mismo tiempo.
Fórmula del módulo volumétrico
Para calcular el módulo volumétrico, se aplica la siguiente fórmula:
Dónde:
K = Módulo volumétrico (Pa)
p = Presión aplicada (Pa)
V = Volumen original
ΔV = Cambio en el volumen
Ejemplo del módulo volumétrico
Los submarinos están fabricados con materiales que poseen un alto módulo volumétrico, lo que les permite soportar presiones extremas provenientes de todas direcciones bajo el agua. El módulo volumétrico de un submarino mide su resistencia a la compresión y se calcula como la razón entre el aumento de presión y la disminución relativa de su volumen.
Este módulo permite determinar cuánto cambiará el volumen de un material cuando se somete a variaciones de presión. Por ejemplo, cuando un submarino desciende desde la superficie del océano hasta el fondo marino, donde la presión es mucho mayor, su volumen se verá afectado. La magnitud del cambio en volumen depende del módulo volumétrico del submarino y de la diferencia de presión.
Los cálculos del módulo volumétrico también son útiles para realizar mediciones relacionadas con la atmósfera y los gases.
Gracias a sensores de presión integrados con los sistemas DAQ de Dewesoft, los ingenieros pueden monitorear los cambios de volumen en los materiales sometidos a compresión. Esta información es esencial en aplicaciones de mecánica de fluidos, diseño de sistemas hidráulicos y pruebas aeroespaciales.
Aplicaciones del módulo volumétrico
Submarinos y otras embarcaciones: Garantizan que los cascos resistan la presión del agua sin sufrir una reducción significativa en su volumen.
Durabilidad del concreto: Dado que el concreto está expuesto a agentes ambientales como humedad, ciclos de congelación-deshielo y cargas mecánicas, conocer su módulo volumétrico es clave para predecir su desempeño a largo plazo.
Sistemas hidráulicos: Asegura que la compresibilidad del fluido no afecte el rendimiento del sistema.
Ingeniería aeroespacial: Se utiliza para evaluar el comportamiento de los materiales ante variaciones de presión a gran altitud.
Investigación en ciencia de materiales: Ayuda en el desarrollo de materiales con propiedades específicas de compresibilidad.
¿Cómo se comparan y se relacionan los módulos elásticos entre sí?
| Módulos elásticos | Definición | Formula | Materiales comunes |
|---|---|---|---|
| Módulo de Young (E) | Mide la rigidez bajo carga axial. | \(E=\frac{\sigma}{\varepsilon}\) | Acero, aluminio, hule |
| Coeficiente de Poisson (ν) | Relación entre la deformación lateral y la deformación axial. | \(\nu= - \frac{\varepsilon_{lateral}}{\varepsilon_{axial}} \) | Hule, espuma, materiales |
| Módulo de corte (G) | Mide la resistencia a la deformación por corte. | \(G = \frac{\tau}{\gamma} \) | Polímeros, aleaciones |
| Módulo volumétrico (K) | Resistencia a la compresión uniforme. | \(K = \frac{-p}{\Delta V / V}\) | Agua, gases |
Los módulos elásticos están interrelacionados y sus relaciones pueden expresarse matemáticamente. Estas ecuaciones permiten a los ingenieros obtener un módulo a partir de otros conocidos, haciendo más eficiente la caracterización de materiales.
El software de Dewesoft integra cálculos matemáticos en tiempo real, lo que permite a los ingenieros calcular el módulo de Young, el módulo de corte y el módulo volumétrico a partir de los datos de esfuerzo y deformación obtenidos. Esta capacidad mejora la eficiencia de las pruebas en aplicaciones de I+D y en entornos industriales.
Preguntas frecuentes sobre los módulos elásticos
¿Cuál es la diferencia entre el módulo de Young y el módulo de corte?
El módulo de Young mide la resistencia de un material a la deformación lineal (axial), mientras que el módulo de corte evalúa la resistencia a la deformación angular (por corte).
¿Cómo se utilizan los módulos elásticos en ingeniería?
Los módulos elásticos se utilizan para predecir el comportamiento de los materiales bajo esfuerzos, asegurando que las estructuras mantengan su resistencia y estabilidad.
¿Qué materiales tienen los valores más altos del módulo de Young?
El diamante, el grafeno y los nanotubos de carbono presentan los valores más altos de módulo de Young.
¿Cuál es la unidad del módulo de corte en el SI?
La unidad del módulo de corte en el Sistema Internacional es el pascal (Pa), aunque comúnmente se expresa en gigapascales (GPa) para materiales de ingeniería.
¿Cómo se calcula el módulo de elasticidad?
El módulo de elasticidad, también conocido como módulo de Young, se calcula con la fórmula: \(E=\frac{\sigma}{\varepsilon}\)
¿Qué es el módulo de elasticidad?
Es una propiedad del material que cuantifica su capacidad de deformarse elásticamente cuando se le aplica un esfuerzo.
Conclusión
Comprender el módulo de Young, el coeficiente de Poisson, el módulo de corte y el módulo volumétrico es fundamental en diversas aplicaciones de la ingeniería y la ciencia. Estas constantes elásticas permiten determinar el comportamiento de los materiales bajo esfuerzo, optimizar el diseño de productos y garantizar la integridad estructural.
Al aprovechar técnicas precisas de prueba y medición, las industrias pueden mejorar la selección de materiales y la eficiencia en su aplicación, lo que se traduce en un mejor rendimiento y mayor seguridad. Con las soluciones avanzadas de adquisición de datos (DAQ) de Dewesoft, los ingenieros pueden medir y analizar con precisión estos módulos, mejorando los resultados en pruebas de materiales y análisis estructurales.