Tabla de contenidos
Examinar las categorías
Buscar autores
 AB
ABAlberto Boffi
 AL
ALAlessia Longo
 AH
AHAl Hoge
 AB
ABAljaž Blažun
 BJ
BJBernard Jerman
 BČ
BČBojan Čontala
 CF
CFCarsten Frederiksen
 CS
CSCarsten Stjernfelt
 DC
DCDaniel Colmenares
 DF
DFDino Florjančič
 EB
EBEmanuele Burgognoni
 EK
EKEva Kalšek
 FB
FBFranck Beranger
 GR
GRGabriele Ribichini
Glacier Chen
 GS
GSGrant Maloy Smith
 HB
HBHelmut Behmüller
 IB
IBIza Burnik
 JO
JOJaka Ogorevc
 JR
JRJake Rosenthal
 JS
JSJernej Sirk
 JM
JMJohn Miller
 KM
KMKarla Yera Morales
 KD
KDKayla Day
 KS
KSKonrad Schweiger
Leslie Wang
 LS
LSLoïc Siret
 LJ
LJLuka Jerman
 MB
MBMarco Behmer
 MR
MRMarco Ribichini
 ML
MLMatic Lebar
 MS
MSMatjaž Strniša
 ME
MEMatthew Engquist
 ME
MEMichael Elmerick
 NP
NPNicolas Phan
 OM
OMOwen Maginity
 PF
PFPatrick Fu
 PR
PRPrimož Rome
 RM
RMRok Mesar
 RS
RSRupert Schwarz
 SA
SASamuele Ardizio
 SK
SKSimon Kodrič
 SG
SGSøren Linnet Gjelstrup
 TH
THThorsten Hartleb
 TV
TVTirin Varghese
 UK
UKUrban Kuhar
Valentino Pagliara
 VS
VSVid Selič
 WK
WKWill Kooiker
Caracterización dinámica de un puente peatonal de dos tramos

Rok Mesar && Daniel Colmenares, Ph.D. and Civil Engineer, Dewesoft Sweden and Jernej Sirk, Application Engineer, Dewesoft HQ.
Kungliga Tekniska Högskolan
August 28, 2025
En la universidad técnica Kungliga Tekniska Högskolan (KTH) en Estocolmo, Suecia, un puente peatonal cruza una carretera y una vía ferroviaria. Recientemente, la universidad se ha asociado con dos empresas, Strusoft y Dewesoft, para estudiar, analizar y monitorear las propiedades dinámicas del puente. Los datos recopilados ayudarán a los estudiantes a aprender cómo evaluar las propiedades dinámicas estructurales de los puentes y ajustar modelos con mayor precisión.

Kungliga Tekniska Högskolan (KTH), el Instituto Real de Tecnología, es la universidad técnica más grande de Suecia. La división de Ingeniería Estructural y Puentes del Departamento de Ingeniería Civil y Arquitectónica de KTH desarrolló este proyecto de monitoreo de puentes. El profesor Raeid Karoumi lidera el proyecto conjunto, que comenzó en septiembre de 2023 con la creación de una base de datos de puentes de código abierto como objetivo principal.
Futuros estudiantes de doctorado podrán utilizar estos datos para aprender a realizar análisis modal experimental (EMA) y operacional (OMA), así como a calibrar modelos matemáticos de elementos finitos (FE) con datos reales. También podrán experimentar cómo diferentes condiciones y cargas afectan el comportamiento dinámico del puente, evaluar su estado estructural y planificar el mantenimiento.



El proyecto conjunto involucra a Strusoft y Dewesoft. Strusoft es una empresa sueca de software que desarrolla herramientas de diseño estructural para ayudar a los ingenieros a analizar, diseñar, fabricar y ensamblar edificios y otras estructuras. Dewesoft es un proveedor esloveno de herramientas de monitoreo, que incluye sensores, dispositivos de adquisición de datos con software y bases de datos.
Dentro del proyecto, KTH se encargó de la instalación e interpretación de los datos, mientras que Strusoft proporcionó el software utilizado para construir el modelo de elementos finitos (FEM) del puente. Dewesoft suministró los acelerómetros, sensores de temperatura, adquisición de datos, la entrada IEPE para realizar pruebas con martillo de impacto y software de análisis, incluyendo Análisis Modal Experimental (EMA) y Análisis Modal Operacional (OMA).
El ingeniero civil Daniel Colmenares Herrera, Ph.D., fue responsable de la parte de KTH, mientras que el M.Sc. En ingeniería civil y planificación urbana, Shaho Ruhani, estuvo a cargo de la parte de Strusoft. La representación de Dewesoft fue liderada por el desarrollador de negocios en monitoreo Rok Mesar y el gerente de país en Suecia, Tobias Ljunggren.
El monitoreo del puente
El puente de dos tramos de KTH proporciona un paso seguro para peatones en la zona de Albano. Conecta el campus de KTH con la ciudad de Estocolmo, atravesando una carretera y las líneas de tren.
Dado que la estructura se encuentra en el campus universitario de KTH, una de las zonas más concurridas de la ciudad de Estocolmo, los criterios de confort son más exigentes. Evaluar el comportamiento dinámico del puente se convierte en una tarea fundamental.
El puente presenta varias frecuencias naturales por debajo de 6 Hz. Este tipo de estructuras pueden mostrar un comportamiento dinámico deficiente cuando están algunas cargas inducidas por el tránsito peatonal y, en algunos casos, superar el estado límite de servicio.
Además, el puente puede presentar diferentes propiedades dinámicas —frecuencias y amortiguamiento— en condiciones climáticas de invierno y verano. Realizar una evaluación dinámica en condiciones operativas y cercanas a la resonancia mejora la toma de decisiones en ingeniería para el mantenimiento.
El monitoreo permite a KTH determinar de manera confiable las propiedades dinámicas del sistema, como frecuencias, amortiguamiento y formas modales. Estos datos posibilitan la calibración de un modelo completo de Elementos Finitos (FE) para distintas condiciones climáticas. La universidad puede hacer un seguimiento de las propiedades inherentes del sistema y compararlas a lo largo del tiempo para obtener evaluaciones más realistas del estado del puente. En general, los ingenieros pueden identificar daños en el puente y tomar decisiones racionales sobre su mantenimiento en una etapa temprana.
El puente KTH
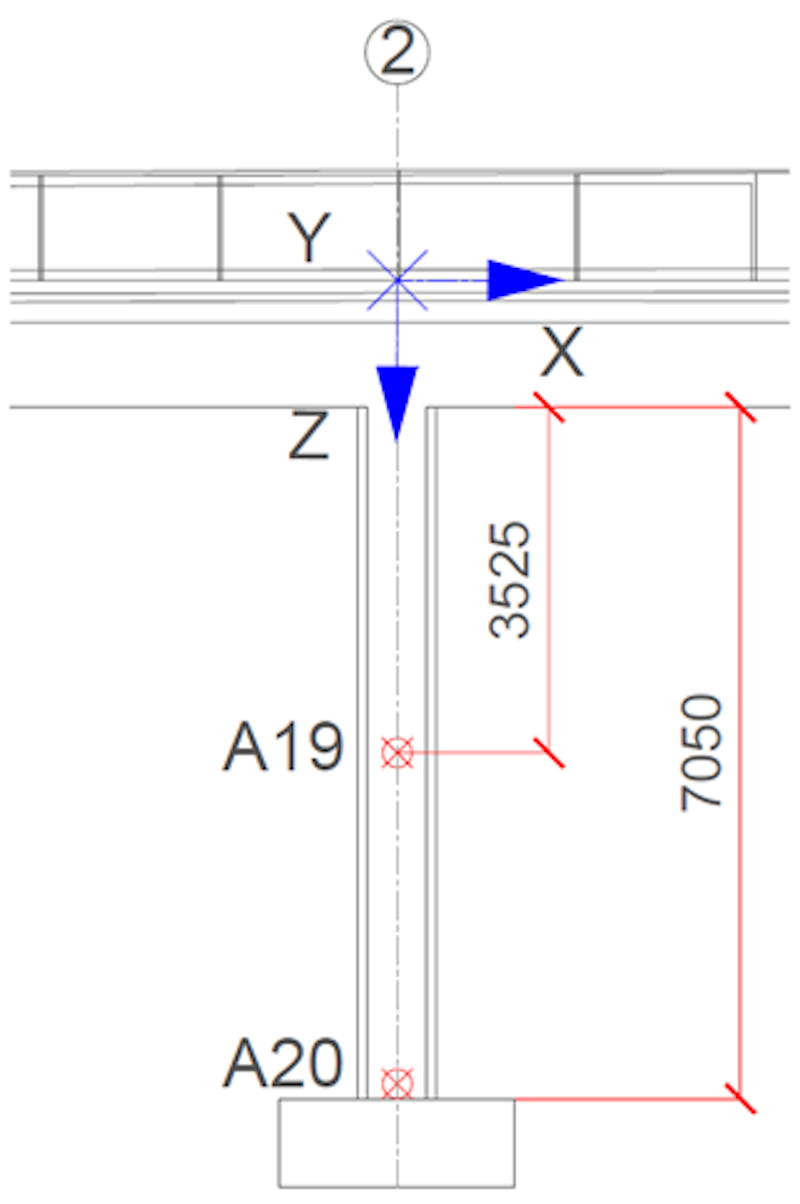
El puente peatonal en KTH consta de una viga de concreto postensado continua de dos tramos, como se muestra en la Figura 2. Cada tramo mide 34,75 m, con un soporte en columna central de 9 m de longitud. El tablero del puente tiene apoyo en los extremos de ambos tramos.
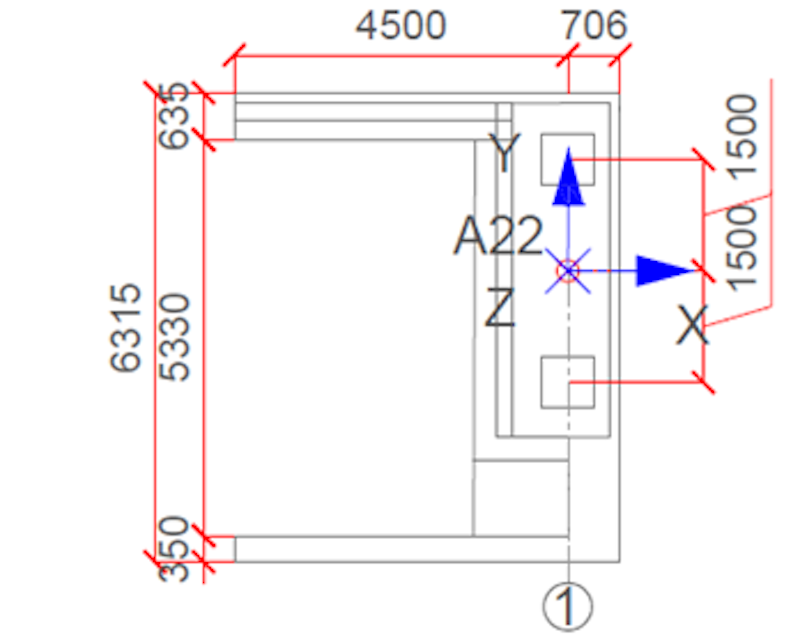
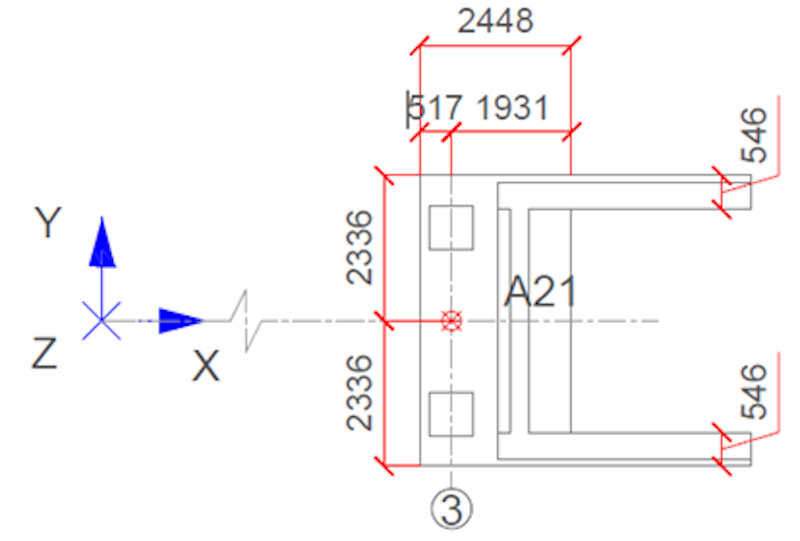
La sección transversal del tablero del puente varía, como se muestra en la Figura 3. La Figura 4 ilustra la variación de la inercia y el área de la sección transversal. El tablero del puente está construido con concreto de clase K45, mientras que la columna de soporte es de concreto K40. No se ha estudiado el efecto de los cables de postensado.
Análisis aproximado de valores propios
Estimamos las propiedades dinámicas del puente utilizando fórmulas de referencia. Para el modo longitudinal del puente descrito, concentramos la masa en la parte superior de la columna de soporte. Incluimos la masa modal de la columna en el sistema equivalente de un grado de libertad (SDOF) concentrado (24,24 % de la masa de la columna). Consulte los resultados en la Tabla 1.
Para el primer modo de flexión, asumimos que la columna de soporte se comportaría como un apoyo articulado, ajustándose a un sistema de viga de dos tramos. De este modo, pudimos estimar su primer modo de flexión como una función seno completa (el segundo modo de flexión de un sistema de viga simplemente apoyada). Consulte los resultados en la Tabla 1.
| L_b [m] | 69.5 |
| E_b [Pa] | 3.40E+10 |
| (assumed) I_b [m^4] | 0.3 |
| L_c (free length) [m] | 7 |
| m_b [kg] | 440160 |
| m_c [kg] | 31104 |
| 24,24 % m_c [kg] | 7539.6096 |
| E_c [Pa] | 3.30E+10 |
| I_c [m^4] | 0.0768 |
| k_c | 3 E_c I_c / L_c^3 |
| f1_long [Hz] | 1.12 |
| f1_bending [Hz] | 1.65 |
Resultados de pruebas de medición anteriores
La Tabla 2 muestra los resultados de la campaña de medición realizada en condiciones climáticas de otoño (15.4°C). Compararemos estos resultados con la nueva campaña de medición realizada a cabo en condiciones invernales (-5°C).
| Mode | Natural frequency [Hz] | Damping [%] |
|---|---|---|
| 1 (Bending) | 1.77 | 1.4 |
| 2 (Bending) | 2.68 | 1.1 |
| 3 (Lateral) | 2.81 | 0.6 |
| 4 (Bending) | 5.61 | 1.1 |
| 5 (Lateral) | 5.37 | 0.7 |
| 6 (Bending) | 7.27 | 2.5 |
Configuración del monitoreo
Las mediciones en campo se llevaron a cabo para analizar y estudiar las propiedades dinámicas y la respuesta dinámica del puente bajo diferentes escenarios de carga. Colocamos los sensores a lo largo del tablero del puente siguiendo un modelo de elementos finitos (FE) para obtener una referencia calibrada de las propiedades dinámicas esperadas del sistema.
Para abordar el comportamiento longitudinal, lateral y vertical del sistema, distribuimos uniformemente 18 acelerómetros triaxiales a ambos lados del tablero del puente. Además, colocamos dos acelerómetros triaxiales en la columna de soporte vertical del puente para incluir y evaluar su comportamiento dinámico y su papel en el sistema global.
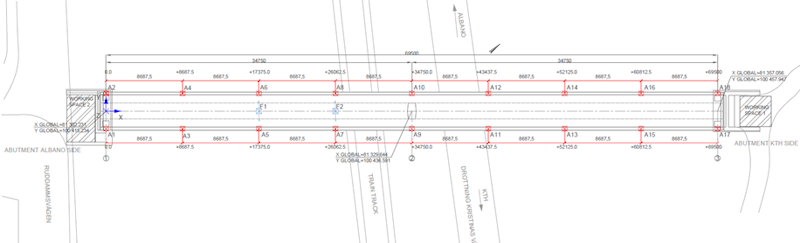
También se instaló un acelerómetro triaxial en cada estribo para evaluar las posibles vibraciones inducidas por los trenes y calibrar el modelo considerando la posible interacción suelo-estructura (SSI). La Figura 5 muestra un esquema del plan de medición, mientras que la Figura 6 presenta la disposición de la instrumentación en el puente. La cantidad y distribución de los acelerómetros seleccionados permite evitar el aliasing espacial en los modos de vibración de orden superior.
Realizamos una prueba de impacto con martillo en las ubicaciones F1 y F2 durante nuestra campaña experimental inicial. Aplicamos una fuerza y utilizamos una ventana exponencial en la señal de impacto y de respuesta, respectivamente, para mejorar la función de coherencia del estimador de la función de respuesta en frecuencia (FRF).
Estimamos las FRF calculando la densidad espectral de potencia de la señal de entrada y la densidad espectral cruzada entre las señales de entrada y salida, siguiendo el estimador H1. Para mejorar la calidad de los FRF, promediamos los resultados de varios impactos con el martillo de percusión.
Procesamos digitalmente los datos medidos, aplicando un filtro pasa banda de fase cero (0.1 a 25 Hz) para la prueba de impacto con martillo. La aplicación de ventanas de fuerza y exponencial mejoró la función de coherencia al optimizar la causalidad de las señales registradas de manera consistente.
De esta manera, minimizamos el doble repique y reducimos el ruido inherente en los datos. Se aplicó un factor de corrección para obtener un estimador adecuado del coeficiente de amortiguamiento, ya que la ventana exponencial introduce un amortiguamiento artificial.
Instrumentación de monitoreo
IOLITEiw-3xMEMS-ACC es un acelerómetro triaxial de baja interferencia (densidad de ruido espectral de 25 μg/√Hz) con un sistema de adquisición de datos (DAQ) integrado e interfaz EtherCAT. Es completamente resistente al agua y cuenta con protección IP67. El dispositivo puede medir aceleraciones estructurales en los ejes X, Y y Z, así como inclinaciones y desplazamientos estáticos.
El IOLITEiw-3xMEMS-ACC-T es un acelerómetro triaxial de baja interferencia (densidad de ruido espectral de 25 μg/√Hz) con un sensor de temperatura digital externo, sistema de adquisición de datos (DAQ) integrado e interfaz EtherCAT. El dispositivo es completamente resistente al agua y cuenta con protección IP67. Puede medir aceleraciones estructurales en los ejes X, Y y Z, así como inclinaciones y desplazamientos estáticos.
IOLITE-1xACC es un acondicionador de señal de alta calidad para sensores IEPE. En este caso, lo utilizamos para leer los datos del martillo de impacto Dytran.
El Dytran 5803A es un martillo de impacto IEPE con una fuerza de impulso definible, diseñado para excitar estructuras de gran tamaño y permitir el estudio de su comportamiento dinámico.
Instalación
El 28 de noviembre de 2023, instalamos el sistema en condiciones climáticas desafiantes, con temperaturas de hasta -5°C y nieve.
Utilizamos soportes de montaje robustos diseñados específicamente para posicionar los acelerómetros en el tablero del puente. Diseñamos previamente dos tipos específicos de soportes para agilizar el proceso de instalación. Estos soportes permitieron colocar los dispositivos de manera eficiente, sin necesidad de tornillos ni adhesivos.
Para las unidades instaladas en las columnas, utilizamos un adhesivo especializado a base de sílice para una fijación segura.


Monitoring software
La solución es una combinación de varios productos de software:
DewesoftX: Software de adquisición de datos: Software de prueba y adquisición de datos para el registro, procesamiento y análisis de señales, así como para la visualización.
Dewesoft Historian: Servicio de software para monitoreo a largo plazo y permanente, incluyendo almacenamiento en una base de datos de series temporales InfluxDB.
Dewesoft Artemis OMA: Un paquete de software para analizar la dinámica estructural de edificaciones, maquinaria en operación y cualquier estructura difícil de excitar de manera controlada. Los parámetros modales, como las formas modales, las frecuencias naturales y los coeficientes de amortiguamiento, pueden determinarse en estructuras en funcionamiento mediante la adquisición únicamente de los datos de respuesta de salida.
Dewesoft Modal Testing and Modal Analysis: Un paquete de software para el análisis de la dinámica estructural de estructuras de ingeniería civil, maquinaria en operación y cualquier estructura excitada artificialmente de manera controlada mediante un martillo de impacto o un vibrador. Los parámetros modales, como las formas modales, las frecuencias naturales y los coeficientes de amortiguamiento, pueden determinarse en estructuras en funcionamiento mediante la adquisición de datos de entrada/excitación y salida/respuesta.
El software incluye funciones para Análisis Modal Experimental (EMA), Formas de Deflexión Operacionales (ODS) y Análisis Modal Operacional (OMA).
Strusoft FEM-Design: Un software avanzado e intuitivo de análisis estructural que satisface todos los requisitos de la ingeniería estructural. Incluye modelado 3D, diseño y análisis de elementos finitos (FEA) para estructuras de concreto, acero, madera, compuestos, mampostería y cimentaciones. Todos los cálculos siguen los estándares del Eurocódigo , con algunos anexos nacionales específicos.
Configuración de medición - OMA (Análisis Modal Operacional)
Para el análisis de aceleraciones, utilizamos un sistema con el software Dewesoft Artemis OMA , un gabinete IP65 con una PC industrial, software DewesoftX , una UPS , PWIN y una fuente de alimentación .
También empleamos sensores MEMS capacitivos triaxiales de baja densidad de ruido .
El dispositivo IOLITEiw-3xMEMS-ACC EtherCAT integra estos acelerómetros. En los puntos donde era necesario medir temperatura y aceleración, instalamos el IOLITEiw-3xMEMS-ACC-T , que además del acelerómetro, incluye un sensor de temperatura. Un microprocesador dentro del dispositivo IOLITE 3xMEMS transmite las muestras al software DewesoftX , que opera en Windows o en cualquier controlador maestro EtherCAT .
Los datos fueron adquiridos a una frecuencia de muestreo de 200 S/s y almacenados en un archivo DXD de 4 horas . Posteriormente, importamos este archivo en Dewesoft Artemis OMA para su análisis.
Pasos del OMA (Análisis Modal Operacional)
Utilizamos el software DewesoftX para la adquisición de datos, asignación de geometría y grados de libertad (DOF). DewesoftX generó un archivo en formato UNF para la exportación de la geometría y un archivo DXD para los datos, los cuales importamos en Dewesoft-Artemis OMA .
En la sección de análisis/preparación de datos , seleccionamos una diezmación a 20 Hz y utilizamos el método EFDD (Enhanced Frequency Domain Decomposition).
Resultados del OMA (Análisis Modal Operacional)
Realizamos un Análisis Modal Operacional (OMA) para extraer las frecuencias naturales , los coeficientes de amortiguamiento y las formas modales del puente.
| Mode | Frequency (Hz) | Damping (%) |
|---|---|---|
| 1st (bending) | 2.22 | 2.1 |
| 2nd (bending) | 3.03 | 2.2 |
| 3rd (lateral) | 6.09 | 0.9 |
| 4th (bending) | 6.97 | 0.8 |
| 5th (bending) | 8.32 | 0.8 |
| 6th (lateral) | 11.39 | 2.1 |
Configuración de medición – EMA (Análisis Modal Experimental)
Aplicamos el Dytran 5803A, un martillo de impacto IEPE, para la excitación artificial. Se identifican dos puntos, F1 y F2, para excitar la estructura (ver Figura 6).
El sistema incluía el software Dewesoft Modal Testing y Modal Analysis, un gabinete IP65 con una PC industrial, el software DewesoftX, un UPS, PWIN, una fuente de alimentación, sensores MEMS capacitivos triaxiales de baja densidad de ruido y un martillo de impacto modal.
Pasos de la EMA (Análisis Modal Experimental)
En el módulo Dewesoft Modal Testing, seleccionamos la excitación con martillo de impacto y la opción de Roving Hammer , lo que nos permitió excitar la estructura en Múltiples puntos. También fue necesario definir la resolución de frecuencia adecuada para determinar el tamaño del bloque de datos en el dominio del tiempo para el cálculo de un bloque. Los principales resultados del módulo MT son la función de respuesta en frecuencia (FRF) y la función de coherencia .
De acuerdo con el plan de medición del puente, debíamos excitar la estructura en dos puntos, por lo que creamos dos canales de excitación (n.º 23 y n.º 24) para la prueba con el martillo de impacto. El nivel de activación se desarrolló en 50N , lo que significa que el software no reconoce impactos por debajo de este nivel. También fue necesario determinar la dirección y orientación de los canales de excitación.
Medimos las respuestas en 22 puntos con acelerómetros triaxiales y creamos 66 canales de respuesta: 22 puntos en tres direcciones. Los ID de nodo, las direcciones y la orientación deben definirse para cada ubicación en consecuencia.
Diseñamos la geometría del puente KTH en el Editor de Geometría . Se pueden crear geometrías definiendo y combinando objetos, importando archivos UNV o posicionando individualmente cada punto de coordinación.
Podríamos animar la geometría de la estructura basada en las FRF adquiridas al seleccionar la frecuencia.
Utilizamos el módulo de análisis modal para extraer los parámetros modales a partir de los datos medidos. Para el cálculo, pudimos usar todas las FRF , y en la configuración del análisis modal definimos el ancho de banda y el orden máximo de los ajustes polinomiales.
Podríamos calcular las formas modales seleccionando manualmente los polos estables en el diagrama de estabilización.
Resultados del EMA (Análisis Modal Experimental)
| Mode (ID) | Dampened frequencies (Hz) | Damping Ratios (%) |
|---|---|---|
| 1 | 2.25 | 0.861 |
| 2 | 3.10 | 0.956 |
| 3 | 6.96 | 0.923 |
| 4 | 8.30 | 1.315 |
| 5 | 13.91 | 1.225 |
| 6 | 15.83 | 1.393 |
Los modos laterales no fueron identificados, ya que la excitación en la prueba con el martillo se realizó en la dirección vertical. Por lo tanto, se activaron los modos verdes.
Modelado por Elementos Finitos
El modelo de Elementos Finitos (FE) nos proporcionó una idea de la incertidumbre asociada con el sistema. Estudiamos la influencia de los cambios de temperatura y sus efectos en las propiedades dinámicas del sistema.
Los cuatro aspectos analizados fueron:
Las variaciones del módulo elástico del concreto.
La influencia de las condiciones de borde elástico.
La influencia de las propiedades mecánicas de la capa de asfalto.
La influencia de la junta de dilatación en las propiedades del sistema.
En este caso, desarrollamos dos modelos:
Modelo basado en cascarón (modelo de ingeniería).
Modelo sólido (modelo de investigación).
Para nuestro modelo de ingeniería, modelamos la losa del puente y la columna con elementos de cascarón 3D de 9 nodos (elementos de Mindlin–Reissner) con un tamaño de malla promedio de 0.1 m . Las vigas de borde se modelaron con elementos de viga 3D de 2 nodos (Timoshenko) con una división de 20 segmentos . El modelo FE no incluyó el efecto del concreto pretensado .
Realizamos un análisis de convergencia en relación con las frecuencias naturales del sistema para investigar la convergencia de la malla seleccionada, sin considerar las barandillas.
Ver el modelo basado en cascarón en la Figura 20 .
Utilizamos el modelo basado en ingeniería para comprender la influencia de la incertidumbre en las propiedades del material del concreto sobre las propiedades dinámicas del sistema. Nos enfocamos en la combinación con el efecto de las condiciones de borde en la estructura, ya que los apoyos de rodillo pueden no estar activos en sus condiciones operativas debido a la fricción en los soportes.
Ver los resultados del análisis paramétrico de las frecuencias naturales del sistema en función del módulo elástico del concreto y las condiciones de borde (- rodillo-rodillo y - pasador-pasador) en la Figura 21 .
Desarrollamos el modelo de investigación utilizando un elemento tetraédrico cuadrático de 10 nodos con un tamaño de malla inicial de 0,6 m. Para las barandillas de acero, que se extienden cuatro metros desde la losa del puente hasta el estribo ( lado KTH ), utilizamos elementos de viga 3D de Euler-Bernoulli con un tamaño de malla inicial de 0,2 m.
Finalmente, la capa de asfalto tiene un espesor constante de 75 mm sobre la losa del puente, sin continuidad más allá de esta.
Ver una imagen del modelo en la Figura 22.
Evaluamos tres aspectos del modelo:
La influencia de las condiciones de frontera.
La influencia de las propiedades del material del asfalto.
La influencia de la junta de dilatación.
Consideramos la influencia de las condiciones de borde asumiendo un resorte lineal en la dirección longitudinal del puente para representar la fricción en el soporte de apoyo en la condición operativa del puente. Los resultados se muestran en la Figura 23 .
Las frecuencias naturales del puente cambian al variar la rigidez del resorte KbK_bKb, lo que revela las propiedades dinámicas del sistema en función de los parámetros seleccionados. Ver las formas modales del sistema utilizando el modelo 3D completo en la Figura 24.
La influencia de la capa de asfalto se analiza variando sus propiedades mecánicas en el puente en función de la temperatura. Ver las propiedades estimadas del material de la capa de asfalto en condiciones cálidas y frías en la Tabla 5.
| T (°C) | v (-) | P (kg/m^3) | E (Gpa) |
|---|---|---|---|
| 40 | 0.40 | 2450 | 1 |
| 0 | 0.20 | 2450 | 17 |
Por lo tanto, calculamos las propiedades dinámicas del sistema variando las propiedades de la capa de asfalto en el modelo de Elementos Finitos . La Figura 25 muestra los resultados del análisis paramétrico de las frecuencias naturales del sistema en función del módulo elástico de la capa de asfalto.
Podemos ver que el efecto de la capa de asfalto no fue tan pronunciado como la rigidez de los soportes de los apoyos del sistema. Cuantificamos la influencia de las juntas de dilatación en las propiedades dinámicas del sistema. Supusimos un recurso lineal que conecta los extremos del puente con sus respectivos estribos, siguiendo la geometría de la junta de dilatación a lo largo de una longitud de 4.35 m (ancho del puente).
Ver los resultados del análisis paramétrico de las frecuencias naturales del sistema en función de la rigidez del resorte elástico de la junta de dilatación en la Figura 26 . Las juntas de dilatación afectan más los primeros y quintos modos de vibración del sistema.
Comparación de resultados
Ver los cambios en las frecuencias naturales del sistema durante las condiciones climáticas de otoño e invierno en la Figura 27.
We saw how the seasonal temperature effect shifts the line of the system’s natural frequencies upwards, leading to a stiffer structure. Moreover, the influence of the previously mentioned aspects affects the bridge’s natural frequencies. See the change ranges accounting for asphalt properties, expansion joint, and bearing spring stiffness vs. the changes due to the temperature effect in Figure 28.
Finally, we quantified the system’s changing damping ratio in autumn and winter weather conditions - see the results in Figure 29.
Conclusiones
Establecimos por qué es necesario realizar mediciones. De otro modo, no sería posible definir una tendencia clara de la relación modal en función de la temperatura.
Podemos explicar la magnitud de los cambios en las frecuencias naturales del sistema debido a los efectos de la temperatura. Es una suma ponderada de los cambios en las propiedades de la capa de asfalto, la rigidez de la junta de dilatación y la rigidez del resorte en los soportes de los apoyos. De esta manera, pudimos presentar el análisis de sensibilidad completo del sistema. Para futuros estudios, podríamos hacer una calibración completa del modelo de Elementos Finitos para cuantificar con precisión las incertidumbres del sistema siguiendo un enfoque basado en la física.
Los resultados muestran cómo las condiciones climáticas pueden tener una influencia significativa en el comportamiento dinámico del sistema. Nuestro caso demuestra la necesidad de modelos más confiables respaldados por campañas de medición en infraestructuras. Monitorear los sistemas estructurales puede ayudar a detectar daños en sus primeras etapas. También puede proporcionar una comprensión más completa de las propiedades reales del sistema construido y calibrar los modelos de Elementos Finitos para mejorar el diseño de los sistemas de gestión de puentes.
Hicimos una comparación entre el modelo de ingeniería y el modelo completo en 3D. Exponemos el problema de la unicidad de la solución para calibrar los modelos y sus limitaciones correspondientes. Podríamos necesitar más mediciones para mejorar y calibrar más los modelos de Elementos Finitos . Por ejemplo, monitoree los desplazamientos de los apoyos agregue información valiosa del sistema a los modelos.
El valor de este trabajo radica en:
Demostrar la influencia significativa que las condiciones climáticas pueden ejercer sobre el comportamiento dinámico del sistema.
Las incertidumbres que pueden surgir en los modelos de Elementos Finitos tanto en un contexto de ingeniería como de investigación.
El monitoreo es esencial para evaluar el rendimiento del sistema y mejorar la práctica actual de ingeniería para los sistemas de gestión de puentes.